Příklad: Vyšetřete konvergenci následující mocninné řady:

Řešení: Vypadá to jako standardní příklad, takže použijeme standardní postup. Nejprve si řadu přepíšeme to příslušného tvaru.

Vidíme, že střed této mocninné řady je a = 2. Teď určíme její poloměr konvergence otestováním absolutní konvergence. Použijeme vhodný test, zde by mělo odmocninové kritérium dobře zafungovat.

Pro členy této mocninné řady jsme použili značení A_k, protože "a_k" (které se obvykle v odmocninovém kritériu používá) je v kontextu mocninných řad vyhrazeno pro koeficienty.

Víme, že řada konverguje absolutně, jestliže je ró menší než 1, podmínka tedy je |x − 2| < 2.

Vidíme, že poloměr konvergence je R = 2.

Interval konvergence je tedy alespoň

(2 − 2,2 + 2) = (0,4).

Nejistý je teď statut krajních bodů, ty je třeba vyšetřit individuálně.

Krajní body:
x = 0: Dosadíme do dané řady (což je obvykle lepší, než dosazovat do "správného" tvaru) a dostaneme řadu

Tato řada je vlastně něco, co už bychom měli znát, protože je to p-řada. V tomto případě p = 1/2 < 1, takže tato řada diverguje. Bod x = 0 neleží v oboru konvergence.

Všimněte si, že toto x leží přesně na hranici oblasti určené poloměrem konvergence, takže kdybychom jej dosadili do vzorce pro ró výše, dostali bychom 1. Nemá tedy smysl zkoušet na tuto řadu odmocninové kritérium nebo podílové kritérium.

x = 4: Dosadíme do dané řady a dostaneme řadu

Jaký test použijeme? Protože členy nejsou všechny kladné, nemůžeme použít obvyklé testy. Přirozenou volbou je zde Leibnizovo kritérium s

Posloupnost {b_k} je kladná, klesající a jde k nule, tudíž zkoumaná řada konverguje. Bod x = 4 tedy náleží do oboru konvergence.

Protože alespoň jeden z krajních bodů v oboru konvergence chybí, nemůže v nich být absolutní konvergence.

Závěr: Daná řada má střed a = 2 a poloměr konvergence R = 2. Její obor absolutní konvergence je (0,4), její obor konvergence je (0,4⟩.

Poznámka: Není třeba přepisovat řadu na "správný" tvar. Střed se najde řešením rovnice

(x/2 − 1) = 0.

Také odmocninové kritérium lze aplikovat na původní tvar řady, pak je na konci třeba přepsat výsledný výraz tak, aby v absolutní hodnotě nebyla před x násobící konstanta. Výsledné ró by pak mělo být stejné. A opravdu,

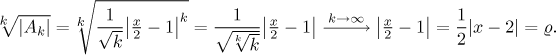
Zdá se tedy, že je vlastně snažší pracovat s řadou tak, jak byla dána, ušeříme jeden krok v řešení. Ve většině případů to tak je v pořádku, ten krok navíc má jeden účel: Potvrdí, že opravdu máme mocninnou řadu, tudíž je náš postup správný. Protože to je ale obvykle zjevné, já osobně volívám ten rychlejší způsob.

Poznámka: Někteří lidé raději určují poloměr konvergence jinak, jmenovitě si pamatují vzorec z příslušné Věty. Budou pak počítat takto.

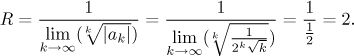
Vynechali jsme ve výpčtu některé kroky, protože jsou evidentně stejné jako předtím. Oba způsoby ( přes odmocninové kritérium nebo přes vzorec z Věty) mají shodný základ, je jen otázka osobní volby, který je lepší. Všimněte si, že výpočet přes vzorec vyžaduje, abychom řadu přepsali do jejího standardního tvaru. To je jeden z důvodů, proč dávám přednost použití odmocninového (či podílového) kritéria způsobem ukázaným v první Poznámce, ušetřím si pak přepisování řady. Druhý důvod je, že si pak nemusím pamatovat ten speciální vzorec, stačí odmocninové kritérium (nebo podílové kritérium), které si už ale stejně pamatuju.

Další příklad
Zpět na Řešené příklady - Řady funkcí