Srovnávací kritéria používáme pro řady, jejichž členy mají části, keré chceme v našich úvahách ignorovat. Základní myšlenka je, že když je nám dána řada, která se nám úplně nelíbí, tak přejdeme k jiné řadě (testovací řadě), jejíž konvergence/divergence je už známá či přínejmenším snadná ke zjištění. Tuto informaci pak převádíme na danou řadu, což ale není vždy možné.
Poznamenejme, že "řada jejíž konvergence je známá" nejčastěji znamená
p-řadu neboli
řadu se členy
Přesná tvrzení ohledně srovnávacích kritérií se najdou v sekci Srovnávací kritéria v části Teorie - Testování konvergence, zde se soustředíme na praktický přístup.
Jsou v zásadě dvě základní situace.
1. Přímé srovnání: Někdy máme řadu, která má omezené části, ty pak
lze nahradit něčím pěknějším. Typické příklady jsou řady, jejichž členy
zahrnují
Jindy chceme zjednodušit složitý výraz tím, že bychom ignorovali některé
jeho části. Pokud toto vede na obecný vzrůst členů (nebo zmenšení), tak je
to zase něco, co srovnání zvládne.
Základní myšlenkou srovnávacího kritéria je, že nerovnost může přejít z jednotlivých členů na řadu:
![]()
pak se použije selský rozum k dosažení závěru: Když je konečné číslo vpravo, musí být i vlevo; když je nekonečno vlevo, musí být i vpravo. Mimochodem, velká písmena používáme záměrně: Tradičně se členy dané řady značí pomocí ak, ale v té nerovnosti výše se může objevit na obou stranách, jako ta menší i jako ta větší. Mátlo by tedy, pokud bychom v té nerovnosti použili také a.
Hlavní problém se srovnávacím kritériem je fakt, že funguje jen "jedním směrem". Ne všechna srovnání, která dostaneme, jsou užitečná. Někdy nemáme moc na výběr a srovnání je vynuceno situací, pak můžeme jen doufat, že to vyjde. Ukázku lze najít v tomto příkladě v části Řešené příklady - Testování konvergence.
Někdy je ale více možností a v takovém případě je velice užitečné, pokud umíte odpověď odhadnout, protože to napoví, jak řešit. Postup je pak následující.
Algoritmus:
Je dána řada∑ ak s nezápornými členy. Rádi byste přešli k jiné řadě∑ bk s nezápornými členy.
• Pokud si myslíte, že daná řada konverguje, pak hledejte horní odhad, abyste ji stlačili dolů, neboli hledejte bk tak, abyak ≤ bk a∑ bk konvergovala.
• Pokud si myslíte, že daná řada diverguje, pak hledejte dolní odhad, abyste ji vytlačili nahoru, neboli hledejte nezáporné bk takové, žeak ≥ bk a∑ bk diverguje.
Hlavní výhodou srovnávacího kritéria je, že členy bk nepotřebují být velmi podobné ak (na rozdíl od limitního srovnání), což umožňuje větší flexibilitu.
2. Limitní srovnání: Limitní srovnání používáme ke zjednodušení členů v situacích, kdy odhadneme, že pro velké hodnoty k přestávají být některé části ve výrazu pro ak důležité. Základní myšlenka limitního srovnávacího kritéria je, že když pro velké hodnoty k členy ak vypadají v zásadě jako nějaké jednodušší (kladné) členy bk, pak se také jejich řady musí chovat podobně.
![]()
Jádrem tohoto kritéria je to odhadování. Zde používáme naši zkušenost s intuitivním výpočtem, daný výraz nahrazujeme jeho dominantním členem (členy). Aby to ale bylo spolehlivé, musíme svůj odhad potvrdit, a potvrzení o shodnosti dvou kvantit pro k blízké nekonečnu se dělá přirozeně: Tyto kvantity mezi sebou vydělíme a pošleme k do nekonečna. Jestliže jsou tyto kvantity stejné, pak očekáváme výsledek 1, ale libovolné kladné číslo postačí.
Algoritmus:
Je dána řada∑ ak s nezápornými členy, které se dají pro velká k zjednodušit.
Krok 1. Odhadněte, jaký je kandidát pro testovací řadu; jinými slovy, odhadněte, že když se k blíží k nekonečnu, pak jsou členy ak v zásadě stejné jako kladná čísla bk.
Krok 2. Potvrďte svůj odhad výpočtem
limita musí vyjít jako kladné reálné číslo (typicky 1, ale ne nutně).
Krok 3. Vyšetřete konvergenci testovací řady∑ bk. Závěr (zda konverguje či diverguje) platí také pro danou řadu∑ ak.
Hlavní výhoda limitního srovnávacího kritéria je, že formálně jde o ekvivalenci, čili informace vždy přechází od testovací řady k dané. Díky tomu je tento test velice robustní. Nevýhody jsou dvě. Jedna je menší, v porovnání se srovnávacím kritériem se obvykle trochu víc pracuje (počítá se ta limita). Druhá nevýhoda je nutnost blízkosti ak a bk, což neumožňuje více tvůrčí nápady.
Příklad: Určete konvergenci řady
![]()
Máme tu přirozené srovnání, jmenovitě
![]()
Bohužel, testovací řada napravo je harmonická řada známá coby divergentní (p-test), což je přesně situace, kdy srovnání selže. A opravdu, ta nerovnost říká, že součet dané řady je menší nebo roven nekonečnu, což je pravda, ať už daná řada konverguje nebo je nekonečná.
Intuitivní přístup naznačuje, že to srovnání výše je velmi věrné, že pro velká k jsou ony dva výrazy prakticky totožné, takže bychom si tipli, že daná řada diverguje. Pokud bychom to chtěli dokázat obyčejným srovnáním, museli bychom pro ni najít dolní odhad, ale takový je zde méně zjevný, protože jde proti "přirozenému" směru předvedenému výše. Mohli bychom zkusit následující:
![]()
Srovnání mezi členy není těžké dokázat, je založeno na tom, že pro přirozená čísla je druhá odmocnina vždy dominována samotným číslem. Řada napravo je teď zároveň menší než ta daná a dává nekonečno, což dokazuje, že je daná řada divergentní.
Naše úvahy také vypadají jako pozvánka pro limitní srovnání. Tvrdíme, že pro velké hodnoty k máme
![]()
To je třeba potvrdit:
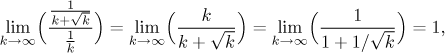
což dokazuje naše tvrzení. Proto se tedy daná řada a harmonická řada chovají stejně, a protože ta druhá je divergentní, musí být i daná řada divergentní.
Pro další příklady viz tento příklad, tento příklad, tento příklad, tento příklad, tento příklad a tento příklad v části Řešené příklady - Testování konvergence.
Odmocninové kritérium
Zpět na Přehled metod - Testování
konvergence