Příklad: Vyšetřete konvergenci následující mocninné řady:

Řešení: Je to opravdu mocninná řada? Ano, dá se přepsat jako

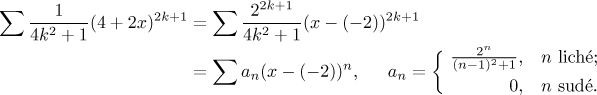
Vidíme, že střed této mocninné řady je a = −2. Můžeme použít standardní postup, začneme s určením poloměru konvergence. Poznamenejme, že ti, kteří dávají přednost Větě, to teď mají těžší, protože se potřebují vyrovnat se těmi nepříjemnými koeficienty a_k. Alternativní způsob, aplikovat vhodný test přímo na danou řadu (viz první Poznámka v předchozím příkladu), takový problém nemá, a proto jej použijeme. Jdeme na to, jako obvykle my mělo dobře fungovat odmocninové kritérium.

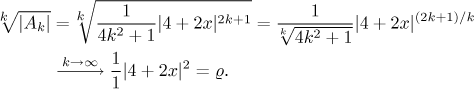
Pro členy této mocninné řady jsme použili značení A_k, protože "a_k" (které se obvykle v odmocninovém kritériu používá) je v kontextu mocninných řad vyhrazeno pro koeficienty. Ve jmenovateli jsme použili faktu, že k-tá odmocnina z polynomu jde vždy k 1.

Víme, že řada konverguje absolutně, jestliže je ró menší než 1, podmínka tedy je

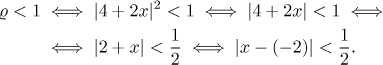
Poloměr konvergence je R = 1/2.

Interval konvergence je tedy alespoň

(−2 − 1/2,−2 + 1/2) = (−5/2,−3/2).

Nejistý je teď statut krajních bodů, ty je třeba vyšetřit individuálně.

Krajní body:
x = −5/2: Dosadíme do dané řady a dostaneme řadu

Jaký test použijeme? Protože členy nejsou všechny kladné, nemůžeme použít obvyklé testy. Přirozenou volbou je zde Leibnizovo kritérium s

Posloupnost {b_k} je kladná, klesající a jde k nule, tudíž zkoumaná řada konverguje.

x = 4: Dosadíme do dané řady a dostaneme řadu

Jaký test použijeme? Tato řada je ukázkovým kandidátem na nějaké srovnání. Šlo by přímé srovnání? Máme přirozený odhad

a řada napravo je konvergentní (viz p-test). Proto podle srovnávacího kritéria konverguje i vyšetřovaná řada.

Oba krajní body tedy náleží do oboru konvergence, provedené výpočty také ukazují, že tam máme i absolutní konvergenci.

Závěr: Daná řada má střed a = −2 a poloměr konvergence R = 1/2. Její obor absolutní konvergence a obor konvergence je ⟨−5/2,−3/2⟩.

Další příklad
Zpět na Řešené příklady - Řady funkcí