Definice limity

Zde zavedeme nejdůležitější pojem spojený s posloupnostmi: pojem limity. Než uvedeme formální definici, pokusíme se nejdříve o intuitivní pochopení.

Připomeňme si příklad geometrické posloupnosti {(1/2)ⁿ}_{n = 0,1,2,...}.

Pokud si spočítáme několik prvních členů a vyjádříme je v desítkovém tvaru, dostaneme

{1, 0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625, 0.0078125, 0.00390625, 0.001953125, 0.0009765625,...}

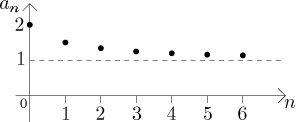
Tento částečný list stejně jako obrázek naznačují totéž: jak se pohybujeme posloupností, členy jsou stále blíže a blíže k nule, vlastně je můžeme dostat jak blízko k nule chceme jen tím, že se podíváme dostatečně daleko. Řekneme, že 0 je limita této posloupnosti; můžeme také říct, že tato posloupnost konverguje k 0. Zhruba řečeno, problém konvergence a limity je vlastně pokus o zodpovězení otázky "co se stane s výrazem a_n, když se n stane velmi velmi velkým." V tomto příkladě máme odpověď: "Když je n opravdu opravdu velké, pak (1/2)ⁿ je přibližně 0."

Použili jsme tohoto příkladu k získání jakési představy, co je to limita. Není to nicméně ten nejvhodnější příklad, protože by mohl naznačit nějaké věci o limitě, které nejsou pravda. Pokusíme se teď ukázat některé populární chybné představy o limitě a naznačit přesněji, co je to limita.

Číslo L je limitou dané posloupnosti {a_n}, jestliže

1. čísla a_n se nakonec dostanou tak blízko k číslu L, jak se nám zachce; jinými slovy, vzdálenost |a_n − L| se nakonec stane menší než libovolná daná tolerance, a
2. vzdálenost |a_n − L| se nejen blíží libovolně blízko k nule, ale nakonec také zůstane tak blízko.

Abychom těmto požadavkům správně rozuměli, podíváme se na dva příklady posloupností, pro které vyznačená hodnota L není limitou:

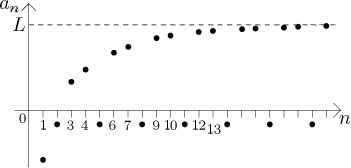
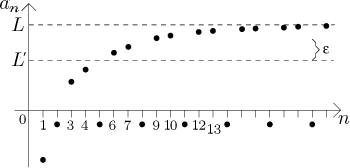
V tomto příkladě posloupnost splňuje podmínku (1). Opravdu, čísla a_n se přibližují k úrovni L a z obrázku to vypadá, že když nám někdo zadá toleranci, jakkoli malou, můžeme najít nějaká a_n, která se od L neliší víc, než je daná tolerance.
Tato posloupnost nicméně nesplňuje podmínku (2), protože každý třetí člen skočí dolů pod osu n, která je daleko od L, a obrázek naznačuje, že se tak děje stále v průběhu celé posloupnosti. Ačkoliv tedy dokážeme najít členy a_n libovolně blízko L, nedokážeme přinutit tuto posloupnost, aby tak blízko zůstala, když se podíváme doprava k jejímu konci.

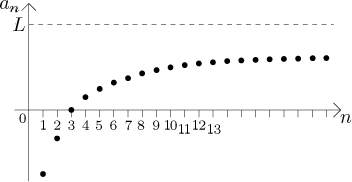
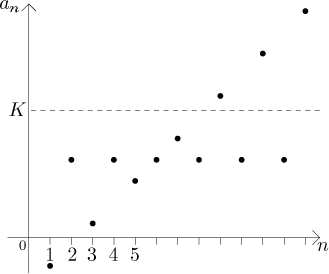
Posloupnost na tomto obrázku splňuje v určitém smyslu (2), neboli blíží se stále blíže k hodnotě L a pak tak blízko zůstane, ale podmínka (1) se nezdá splněna; obrázek naznačuje, že se růst posloupnosti vyrovnává příliš brzy na to, aby došla až k hladině L (i když by samozřejmě bylo nebezpečné dělat závěry jen na základě obrázku; možná se tato posloupnost k L nakonec přiblíží, ale dělá to velmi pomalu; my prostě nevíme).

Tento druhý příklad je zajímavý ještě z jednoho hlediska. V mnoha knihách, když chtějí říct slovy, co je to limita, řeknou: Limita je číslo, ke kterému se daná posloupnost blíží víc a víc. Někdy to dokonce sám používám, protože je to krátké a jakousi představu to dává. Může to být ale zavádějící, protože na posledním obrázku se členy posloupnosti blíží blíž a blíž k hodnotě L, přesto to není limita (zdá se). To o "libovolné blízkosti" je velice podstatné.

Existuje způsob, jak obě podmínky vyjádřit. Zkusíme například toto:

Když nám někdo dá toleranci (tradičně značenou řeckým epsilonem ε), jakkoli malou, my musíme být schopni vynechat nějaký začátek posloupnosti tak, aby ten zbytek, její "konec", již zůstal od L vzdálen maximálně o onu toleranci.

U prvního nekonvergentního obrázku vidíme, že když nám někdo dá toleranci ε = L neboli přesně vzdálenost od úrovně L k ose n, pak ať už vynecháme jakkoli velký začátek posloupnosti, vždy se v tom zbytku najdou členy, které skočí pod osu n a nebudou tedy v tolerované vzdálenosti od L.

Ve druhém obrázku můžeme zvolit za ε řekněme polovinu vzdálenosti mezi úrovní L a úrovní, na které se posloupnost jakoby vyrovnává.

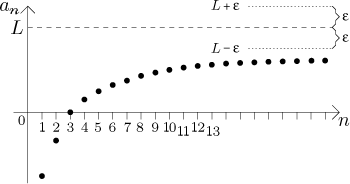
Je zjevné, že nezáleží na tom, jak velký začátek posloupnosti odsekneme, konec nikdy nezůstane v dané toleranci od L, dokonce tam nezasáhne jediným členem (alespoň to tak vypadá).

Teď tedy víme, co to znamená mít limitu. Je neméně důležité vědět, jaké podmínky pro limitu nejsou vyžadovány. Abychom předešli častým nedorozuměním, zdůrazňujeme následující:

Když posloupnost konverguje k limitě L, pak se nevyžaduje, aby se k ní blížila nějakým určitým způsobem.

Například náš první příklad {(1/2)ⁿ}_n=0,1,2,... měl limitu 0 a členy se k této limitě blížily shora a postupně, posloupnost byla klesající. To je velmi speciální případ a je ve skutečnosti příliš pěkný na to, aby nám dal správnou představu o limitě. Pro tu se podíváme na následující příklad:

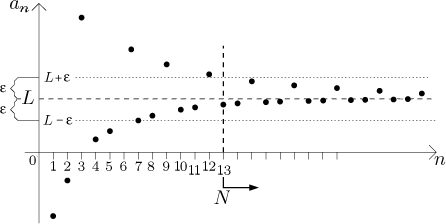
Všimněte si několika věcí. Tato posloupnost je vlastně kombinací dvou trendů. Podobně jako u obrázku prvního nekonvergentního příkladu, i zde každý třetí člen "odskočí", tentokráte ovšem ne pod osu n, ale docela daleko nad úroveň L. Když tyto odskakující členy odmyslíme, tak ty, které zbydou, tvoří pěknou posloupnost, která vypadá, že se blíží k úrovni L zdola po hezké křivce. Co ale lze říct o celé dané posloupnosti? Všimněte si, že ačkoliv každý třetí člen odskakuje, v tomto případě jsou tyto odskoky postupně blíže a blíže k hodnotě L. Tvrdíme, že celá daná posloupnost z obrázku konverguje k L. Podmínka (1) je evidentně splněna a tentokráte funguje i podmínka (2).

Zkusíme se na to podívat z pohledu epsilonového popisu. Když nám někdo dá toleranci ε jako na obrázku, podíváme se, kolik "pěkné části" musíme odříznout, aby zbytek zůstal v mezích daných tolerancí, z také kolik z "odskakujících" členů musíme vyhodit. Nakonec uvidíme, že musíme odříznout začátek posloupnosti, jak je to znázorněno tlustou svislou čárou, a zbytek již zůstane v tolerovaných mezích. Index, u kterého odřízneme začátek, je důležitý, tradičně se značí písmenem N. V našem obrázku máme N = 12 a vidíme, že oříznutá posloupnost {a₁₂, a₁₃, a₁₄, a₁₅,...} zůstává v mezích daných tolerancí.

Teď jsme připraveni na formální definici.

Všimněte si, že ze zápisu limity nevidíme, kde vlastně indexování začíná. Také to není třeba: limita posloupnosti (pokud nějaká existuje) nezáleží na prvních členech dané posloupnosti, pouze na členech "na konci". Když mluvíme o limitě, tak dokonce často vynecháváme i tu část "pro n jdoucí do nekonečna", protože když pracujeme s posloupností, tak n nemůže vlastně jít někam jinam. Pro další detaily o značení viz tato poznámka.

Nejlepší způsob, jak této definici rozumět, je podívat se na ni jako na hru. Někdo - váš protivník - vybere toleranci ε, typicky vybírá velice malé číslo, aby vám to ztížil. Váš úkol je zajistit, že posloupnost zůstane v mezích daných tou tolerancí, a to odříznutím jejího začátku. Jinými slovy, máte najít "odřezávací index" N splňující podmínku, že když se podíváme na a_N a všechny následující členy posloupnosti, budou se od L lišit o méně, než je daná tolerance.

V posledním příkladě jsme vlastně naznačili důkaz z definice, že daná posloupnost konverguje k L. Udělali jsme ale jen jeden krok. Podstatná věc u definice je, že musíte být schopní vyhrát tuto hru, ať už je zvolené epsilon jakkoliv malé, jinými slovy pro jakékoliv kladné epsilon. Z obrázku se zdá jasné, že když někdo zadá menší epsilon než to z obrázku, budeme muset posunout bod odříznutí dále doprava, ale bude možné jej najít.
Porovnejte toto s druhým obrázkem posloupnosti nekonvergující k L. Když je tam zvoleno epsilon docela velké, je možné hru vyhrát. Když ale někdo zvolí epsilon malé, hru nejde vyhrát.

Konvergentní posloupnosti jsou "pěkné". Jejich hlavním rysem je, že členy a_n je možné pro velké hodnoty n nahradit číslem L bez velké chyby. Přesněji, pokud někdo zadá maximální tolerovatelnou chybu, pak víme, že stačí odříznout určitý počet prvních členů posloupnosti a zbytek může být nahrazen číslem L bez překročení této chyby.

Příklad: Tvrdíme, že

Posloupnost začíná (v desetinném tvaru) {2, 1.5, 1.333..., 1.250, 1.200, 1.166..., 1.1428...,...}, takže to tvrzení nevypadá podezřele. Obrázek je

Pro formální důkaz správnosti limity klikněte sem.

Existuje alternativní způsob znázorňování posloupností a limit, který se bude hodit později, když dojde na funkce. Najdete jej v této poznámce.

Při zkoumání posloupností je důležité vědět, co může způsobit, že posloupnost diverguje. Jsou dva základní důvody:

Oscilace, jejíž velikost se nezmenšuje k nule. Vzpomeňme tento příklad:

Členy této posloupnosti oscilují (pro velká n) zhruba mezi úrovněmi L a -L/5. Velikost této oscilace tedy zůstává velká. Ukázali jsme si, že L naznačené v obrázku není limitou. Podobný argument by ukázal, že žádné číslo L' nemůže být limitou, protože když zvolíme L' odlišné od L, pak body této posloupnosti, které jdou blíže a blíže k L, zůstanou daleko od tohoto nového L'. V obrázku znázorňujeme ε, pro které nepůjde vyhrát hru z definice, když se pokusíme dokázat, že L' je limita.

Neomezený růst. Vzpomeňme příklad geometrické posloupnosti {2ⁿ}_n=0,1,2,....

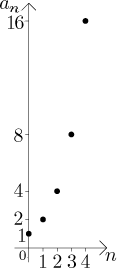
Víme z Teorie - Úvod - Důležité příklady, že tato posloupnost není omezená shora. Když si teď v obrázku představíte vodorovnou linii ve výšce L, mělo by být jasné, že posloupnost od ní "uteče", takže toto zvolené číslo L nemůže být limitou. Pro přesnější důkaz se podívejte sem.

V této situaci lidé často řeknou, že posloupnost "vybouchla". Může také vybouchnout směrem dolů, když jsou její členy stále větší v absolutní hodnotě, ale se záporným znaménkem. Posloupnost také může vybouchnout v obou směrech najednou, pak má ovšem také velké oscilace, jak se některé členy stávají velikými a jiné "velmi zápornými".

Každá posloupnost, která nekonverguje, v sobě obsahuje jedno či obě z těchto dvou chování. Existuje ovšem jeden typ divergující posloupnosti, kdy ještě dokážeme získat užitečnou informaci. Jmenovitě v posledním příkladě šly členy postupně nahoru bez nějaké meze. Zatímco to "postupně" není podstatné, tendence "jít nahoru a nakonec tam zůstat" je velmi užitečná a zaslouží si jméno.

Zde hra funguje následovně. Pro nekonečnou limitu někdo vybere hladinu K, typicky velice velké číslo. Abychom hru vyhráli, musíme najít bod odříznutí N, aby konec posloupnosti a_N, a_N+1, a_N+2,... zůstal nad touto hladinou K.

Pro mínus nekonečno někdo vybere úroveň K, typicky velké číslo se znaménkem mínus ("daleko dole" v obrázku). Abychom vyhráli hru, musíme najít bod odříznutí N, aby konec posloupnosti a_N, a_N+1, a_N+2,... zůstal pod touto úrovní K.

Teď se podíváme na pár příkladů:

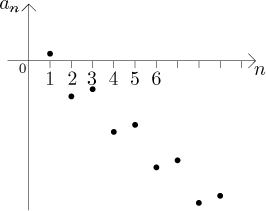
V tomto příkladě není posloupnost monotonní, dokonce osciluje způsobem, který vypadá pravidelně, ale jak tak jde, tak se nakonec dostane pod libovolnou úroveň, která nás napadne. Podle definice tedy jde do mínus nekonečna.

Tato posloupnost není omezená shora, takže ji podezříváme, že konverguje do nekonečna, ale každý druhý člen odskakuje dolů. Zdá se tedy, že některé hry dokážeme vyhrát, ale když někdo zvolí K jako na obrázku, nebudeme schopni odříznout začátek tak, aby zbytek zůstal nad K; vždycky budou členy, které skočí níže. Tato posloupnost tedy nejde do nekonečna, nemá vlastně žádnou limitu.

Ačkoliv posloupnosti v obou příkladech divergují podle první definice limity (všimněte si, že pro ani jednu z nich neexistuje reálné číslo L, které by fungovalo jako limita), vidíme, že když máme limitu nekonečno (či mínus nekonečno), dostáváme užitečnou informaci, která nám dovoluje si o dané posloupnosti něco představit.

Máme teď dvě rozdílné definice limity, podle toho, jakou limitu hledáme. Zkusíme teď do toho vnést nějaký systém.

Vlastně tedy máme dvě rozdílné terminologie, které se částečně překrývají. Existence limity znamená, že posloupnost má jasnou tendenci pro n jdoucí do nekonečna; členy posloupnosti se buď téměř rovnají určitému číslu či mají tendenci jít bez omezení nahoru (nebo dolů) a zůstat tam, ale mají nějakou takovou určitou tendenci. Posloupnosti, jejichž limita neexistuje, nemají jasnou tendenci; mohou mít dvě konfliktní tendence (viz zatím poslední obrázek) nebo je to ještě horší.

Na druhou stranu, konvergentní posloupnost má vlastnost, že pro velká n je možné její členy nahradit vhodným číslem - její vlastní limitou samozřejmě. Divergentní posloupnosti tuto vlastnost nemají. Protože nekonečno není pořádné číslo, posloupnosti, které jdou do nekonečna či mínus nekonečna, nemohou být klasifikovány jako konvergentní, i když mají limitu (nevlastní). A i kdybychom se rozhodli vzít nekonečno mezi čísla (což v určitém smyslu uděláme), pořád nemůžeme členy takové posloupnosti nahradit nekonečnem bez udělání velké chyby; například kdybychom zkusili nahradit 2ⁿ nekonečnem, uděláme velikou chybu, nezávisle na tom, kolik je n; proto je tato posloupnost divergentní, i když má limitu (nekonečno).

Poslední poznámka: Když lidé používají "šipkové značení", často zcela vynechají tu část "pro n→∞". Konec konců, kam jinam by n mohlo jít? Obvykle tedy píšeme jen (1/2)ⁿ→0 či 2ⁿ→∞.

Když napíšeme a_n→L nebo řekneme, že "L je limita" bez bližší specifikace, pak L může být reálné číslo, ale také (plus či mínus) nekonečno. Většina vlastností totiž platí jak pro vlastní, tak pro nevlastní limitu, takže má smysl používat společný zápis. Je tady ovšem rozdíl v tom, jak to čteme. Můžeme říct, že "a_n konverguje k L", pouze pokud víme, že L je vlastní limita neboli reálné číslo. Obecně říkáme, že "a_n jde k L".
Na druhou stranu, pokud posloupnost {a_n} nemá limitu, tak píšeme "lim(a_n) neexistuje".

V této poznáme jsme hovořili o alternativním způsobu kreslení posloupností. Také tam uvádíme jiný způsob, jak se dívat na limitu, alternativní definici chcete-li. Doporučujeme, ať se na to mrknete.

Tuto část uzavřeme tvrzením, které není zrovna dvakrát užitečné v praxi, ale ukazuje, že pojem limity je rozumný:

Věta.
Pokud má posloupnost limitu, je tato limita jednoznačně určená.

Jinými slovy, posloupnost nemůže mít dvě různé limity.

Důležité příklady
Zpět na Teorie - Limita