Definiční obor reálných funkcí: Přehled metod

Kdykoliv zkoumáme danou funkci, vždy začneme definičním oborem, protože všechny další výpočty se budou dít vzhledem k tomuto definičnímu oboru.

Abychom našli definiční obor, zkusíme zodpovědět tuto otázku: Jaká čísla by mohla dělat potíže ve výrazu, který funkci definuje? Protože typická funkce je jen několik elementárních funkcí pospojovaných pomocí kompozice a algebraických operací, stačí projít všechny zúčastněné funkce a operace, některé z nich způsobí omezení pro proměnnou.

Aby se to dalo dělat efektivně, měli byste být dobře obeznámeni s definičními obory elementárních funkcí. Musíte si také pamatovat, že všechny obecné mocniny (tj. mocniny, ve kterých se x vyskytuje jak v základu, tak v exponentu) a odmocniny je nejprve třeba převést pomocí triku z = e^ln(z), teprve pak je můžeme analyzovat.

Seznam typických problémů:

• ve zlomku nesmí být jmenovatel nulový;
• argument logaritmu musí být kladný;
• argument sudé odmocniny musí být nezáporný (tj. kladný nebo nula);
• argument mocniny s obecným (reálným) exponentem musí být kladný;
• argument tangensu nemůže být  + kπ, argument kotangensu nemůže být kπ;
• argument arcsinu a arccosinu musí být z intervalu ⟨−1,1⟩;
• argument hyperbolického kotangensu nemůže být nula;
• argument argcosh musí být z intervalu ⟨−1,∞);
• argument argtgh musí být z intervalu (−1,1);
• argument argcotgh musí být z intervalu (−∞,−1) ∪ (1,∞).

Další elementární funkce (které nejsou na tomto seznamu) jsou definovány pro všechna reálná čísla, proto si nevynucují nějaké omezení pro definiční obor.

Takže prostě projdeme daný výraz a koukáme se po zdrojích problémů, každý nám dá nějakou podmínku k vyřešení. Tato řešení se pak protnou, čímž dají hledaný definiční obor. Proč zrovna průnik? Aby daná funkce existovala, musí všechny její části fungovat současně.

Vlastně jediná netriviální část hledání definičního oboru je řešení obdržených nerovnic. Pokud si tuto středoškolskou látku potřebujete osvěžit, zkuste Řešení rovnic a nerovnic v části Extra.

Než se posuneme k příkladu, je zde myslím čas něco vysvětlit. Ten příklad vypadá strašidelně, ale to je schválně. Rozhodně to není "typický" příklad na definiční obor, takové najdete spíš v sekci Řešené příklady a ve Cvičeních. Zde jsme v sekci Přehled metod, a tak se namísto toho podíváme na funkci se spoustou problémů, abychom si je tu přehlédli. Tento příklad má ještě jeden účel. I když vypadá hrozně, když se podíváte blíže, zjistíte, že ve skutečnosti není obtížnější než ony "typické" příklady, jen je delší, protože se toho musí víc probrat. Tento příklad také ukazuje, že je důležité si v řešení udržet pořádek. Pokud to dokážete a pokud jste se na definiční obory dostatečně podívali, pak vás tento příklad dokonce může povzbudit, když zjistíte, že si poradíte i s takovouto příšerou. A jestli dokážete tohle, pak dokážete udělat všechno, co na vás přijde. Konec povídání, jde se na to.

Příklad: Nalezněte definiční obor

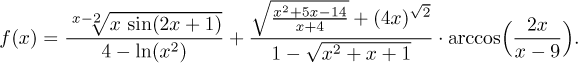
Řešení: Nejprve musíme funkci přepsat tak, aby se v ní nevyskytovaly obecné mocniny.

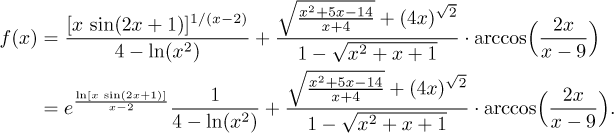
Teď se podíváme po zdrojích problémů. Je tam docela dost polynomů, ale ty spolknou libovolný argument, a tak nás netrápí. Víme také, že exponenciála a sinus berou cokoliv, takže ani tam nebudou problémy. Kde tedy budou? Vezměme to odleva.

1. V exponenciále vidíme zlomek, jeho jmenovatel nesmí být nula. Dostaneme tedy podmínku (x − 2) ≠ 0.
2. V téže exponenciále vidíme logaritmus. Jeho argument musí být kladný, máme tedy podmínku x⋅sin(2x + 1) > 0.
3. Teď je na řadě zlomek, víme, že jeho jmenovatel nesmí být nula, tedy dostaneme podmínku (4 − ln(x²)) ≠ 0.
4. V témže jmenovateli je logaritmus, podmínka tedy je x² > 0.

5. Jako další máme další zlomek, což znamená další podmínku na jmenovatel:

   

6. V témže jmenovateli je druhá odmocnina, podmínka je (x² + x + 1) ≥ 0.

7. V témže zlomku máme druhou odmocninu v čitateli; to vyžaduje

   

8. Zlomek pod touto odmocninou vyžaduje, že (x + 4) ≠ 0.
9. Pořád ještě v tomto čitateli je vedle zlomku (4x) umocněno na mocninu "odmocnina ze 2". Protože exponent - odmocnina ze 2 - je kladné reálné číslo, ne nějaký speciální případ (jako třeba kladné celé číslo), musíme vyžadovat, že (4x) ≥ 0.

10. Konečně se dostáváme k arkuskosinu. Zde je podmínka

    

11. A opravdu nakonec, v tomto zlomku musíme chtít, aby jmenovatel nebyl nula, tj. (x − 9) ≠ 0.

Tím máme hotov seznam problémů. Teď musíme vyřešit těchto 11 podmínek.

Podmínka 1. To jasně říká x ≠ 2.

Podmínka 2. Máme součin dvou členů a víme, že aby byl kladný, jsou dvě možnosti: Buď jsou oba členy kladné, nebo oba záporné. K témuž závěru můžeme dojít, pokud použijeme jinou metodu řešení této nerovnosti. Může nás napadnout vydělit obě strany x⋅sin(2x + 1) > 0 členem x, což by tu nerovnost docela zjednodušilo. Když ale dělíme (či násobíme) nerovnici číslem, musíme se zeptat, zda je kladné či záporné, a v druhém případě prohodit směr nerovnosti. Zde nevíme, proto musíme ověřit oba případy a dát odpovědi dohromady. Ať už řešíme jakkoliv, odpověď je

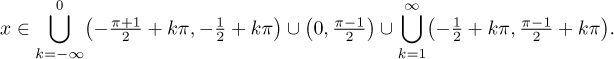
Pro detaily viz tato stránka.

Podmínka 3. Podmínku přepíšeme na ln(x²) = 4. Můžeme na obě strany aplikovat exponenciálu a dostaneme e^ln(x2) = e⁴, neboli x² = e⁴. To má dvě řešení, x = e² a x = −e². Proto je řešením třetí podmínky x ≠ ±e².

Všimněte si, že algebraicky bychom mohli psát ln(x²) = 2ln(x), ale z pohledu funkcí jsou to velmi rozdílné výrazy. Zatímco první z nich (ten daný) existuje pro všechna x ≠ 0, druhý existuje jen pro x > 0. Jako důsledek dostaneme, že zatímco ln(x²) = 4 má dvě řešení, jak už jsme viděli, rovnice 2ln(x) = 4 má jen jedno řešení, x = e²! To ukazuje, že je vždy třeba řešit daný výraz, a když už ho algebraicky měníme, můžeme dělat pouze změny, které neovlivní definiční obor, jinak můžeme ztrácet řešení (či dostávat nesprávné navíc).

Podmínka 4. Tato podmínka má snadné řešení x ≠ 0.

Podmínka 5. Přepíšeme ji do tvaru

Dostaneme tedy dvě podmínky, x ≠ 0 a x ≠ −1.

Podmínka 6. Ověříme, že polynom x² + x + 1 nemá kořeny, proto je buď vždy kladný, nebo vždy záporný. Protože jeho grafem je nahoru otočená parabola (znaménko před x² je "+"), platí to první. Výraz x² + x + 1 je kladný pro všechna reálná čísla a z šesté podmínky tedy nevyplývají žádná omezení na x.

Podmínka 7. Tento typ nerovnice se nejlépe řeší tak, že se výraz rozloží na faktory a pak se určí znaménka jednotlivých faktorů. Je také možné zkusit vynásobit nerovnost jmenovatelem, což by ale vyžadovalo, že vyzkoušíme obě možnosti znaménka pro tento jmenovatel, neboli museli bychom tuto nerovnost řešit dvakrát. Ať už to zkusíte jakkoliv, odpověď je

x∈⟨−7,−4) ∪ ⟨2,∞).

Pro detaily viz tato stránka.

Podmínka 8. Ta zjevně říká x ≠ −4.

Podmínka 9. Zde podmínka evidentně říká x > 0.

Podmínka 10. Tato podmínka jsou vlastně dvě nerovnosti, které se musí řešit současně. Jsou dvě rozumné strategie. Jedna je zbavit se zlomku pronásobením. To se dá udělat současně u obou nerovností, takto vzniklé jednodušší nerovnosti se pak řeší individuálně. Nevýhoda tohoto přístupu je, že se musí udělat dvakrát, pro kladný a záporný jmenovatel.

Alternativou je řešit každou rovnici zvlášť, nejlépe změnou v nerovnost s "0" na jedné straně a součinem/podílem lineárních faktorů na straně druhé, protože pak lze použít metodu určování znaménka tabulkou. Každopádně odpověď by měla být

x∈⟨−9,3⟩.

Pro detaily viz tato stránka.

Podmínka 11. Ta evidentně říká x ≠ 9.

Zbývá dát všechny ty podmínky dohromady. Protože aby existovala, musí mít funkce všechny části bez problémů, vezmeme průnik těchto jedenácti podmínek. To se nejlépe dělá graficky.

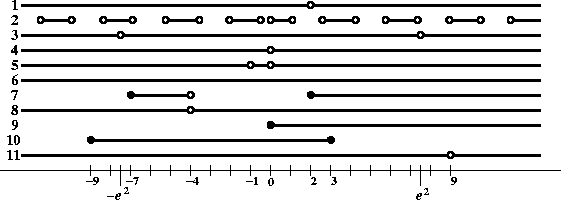
Závěr tedy je, že

Pro další příklady odkazujeme na Řešené příklady.

Omezenost
Zpět na Přehled metod - Základní vlastnosti reálných funkcí