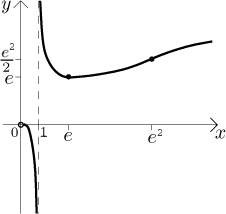
Příklad: Načrtněte průběh funkce

Řešení: Použijeme postup popsaný v sekci Přehled kreslení grafů v části Přehled metod - Průběh funkce.

Krok 1. Definiční obor této funkce je dán dvěma podmínkami. Za prvé, logaritmus vyžaduje, aby x > 0; za druhé, zlomek potřebuje ln(x) nenulové, což znamená, že nemůžeme mít x = 1. Odtud již dostaneme definiční obor.

D( f ) = (0,1) ∪ (1,∞).

Funkce je na něm spojitá. Protože tato množina není symetrická vzhledem k počátku, tak daná funkce nemůže být symetrická.

Průsečíky s osami: f (x) = 0 jedině pokud je čitatel nulový, ale x = 0 je vyloučeno kvůli logaritmu ve jmenovateli. Nejsou tedy průsečíky s osou x a také ani s osou y, jelikož 0 není v definičním oboru.

Krok 2. Najdeme limity v krajních bodech intervalů definičního oboru.

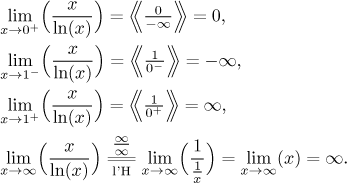
Asymptoty: Jsou dva kandidáti na svislou asymptotu, vlastní krajní body x = 0 a x = 1. Protože jednostranná limita v 0 konverguje, není tam svislá asymptota. V 1 je nevlastní jednostranná limita (dokonce obě, ale jedna stačí), takže je v bodě x = 1 svislá asymptota.

Protože limita v nekonečnu diverguje, není tam vodorovná asymptota, ale limita existuje a tudíž je tam šance na šikmou. Použijeme příslušný algoritmus.

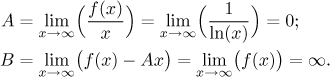
Limita pro A konverguje, takže pořád byla šance, ale limita pro B diverguje a proto není v nekonečnu šikmá asymptota. Mimochodem, k tomuto závěru jsme mohli dojít podle první limity, bez výpočtu B; jediné A, které by mohlo fungovat, je A = 0, ale to by znamenalo vodorovnou asymptotu a tu už jsme vyloučili.

Krok 3. Najdeme derivaci a použijeme ji k určení monotonie a lokálních extremů.

Kritické body: V definičním oboru nejsou body, kde by derivace neexistovala; derivace je nula když ln(x) = 1, tj. v bodě x = e. Dva intervaly definičního oboru se tak rozdělí na tři intervaly monotonie, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

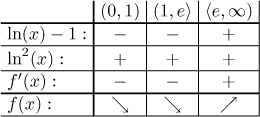
Máme sousedící intervaly stejné monotonie, ale protože bod dotyku 1 je vlastně dírou v definičním oboru, nelze je spojit v interval, ať už f jde jakkoliv. Závěr je, že f je klesající na (0,1) a na (1,e⟩ a rostoucí na ⟨e,∞).

Lokální extrémy: Daná funkce má lokální minimum f (e) = e.

Krok 4. Najdeme druhou derivaci a použijeme ji k určení konvexity.

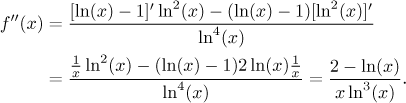
Dělící body: V definičním oboru nejsou body, kde by druhá derivace neexistovala; druhá derivace je nula, když ln(x) = 2, tj. pro x = e². Dva intervaly definičního oboru se tak rozdělí na tři intervaly konvexity, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

Závěr je, že f je konkávní na (0,1) a na ⟨e²,∞); je konvexní na (1,e²⟩.

Inflexní bod: f (e²) = e²/2.

Krok 5. Teď to dáme všechno dohromady. Nejprve načrtneme do obrázku všechny body a limitní trendy, které jsme našli. To bude kostra, na kterou pak funkci pověsíme.

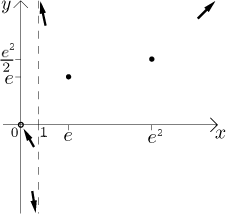
Abychom si tvar grafu lépe představili, zkombinujeme ony dvě tabulky výše.

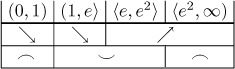
Abychom udělali obrázek věrnější, najdeme limitu derivace v 0 zprava.

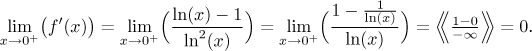
To nám říká, že jak graf vyráží z počátku, tak se "tulí" k ose x. Teď jsme připraveni nakreslit průběh funkce.

Další příklad
Zpět na Řešené příklady - Průběh funkce