Příklad: Načrtněte průběh funkce

Řešení: Použijeme postup popsaný v sekci Přehled kreslení grafů v části Přehled metod - Průběh funkce.

Krok 1. Protože arkustangens akceptuje libovolný argument, jediný problém je se zlomkem. Definiční obor tedy je

D( f ) = (−∞,0) ∪ (0,∞)

a funkce je na něm spojitá. Protože jediné místo, kde se objevuje proměnná, je v sudé mocnině, je tato funkce sudá. Opravdu je snadné ověřit, že f (−x) = f (x).

Průsečík s osou x: Arctg je nulový pouze tehdy, je-li jeho argument nula, což není možné. Nejsou tedy průsečíky s osou x, a protože 0 není v definičním oboru, není také průsečík s osou y.

Krok 2. Najdeme limity v krajních bodech intervalů definičního oboru.

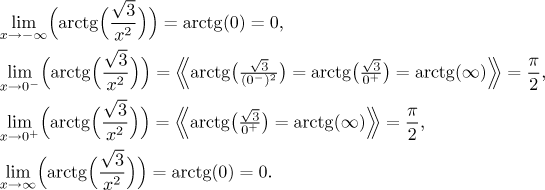
Protože je funkce sudá, tak vlastně stačí spočítat jen první dvě limity a ty druhé dvě vyplynou ze symetrie funkce. Vidíme, že bychom vlastně mohli "zaplnit" díru v grafu, tj. pokud bychom také definovali f (0) = π/2, dostali bychom spojitou funkci na celé reálné ose.

Asymptoty: Protože je funkce na svém definičním oboru spojitá, jediným kandidátem na svislou asymptotu je vlastní krajní bod x = 0. Tam ale máme vlastní limitu, takže svislé asymptoty nejsou.

Protože limity v mínus nekonečnu a v nekonečnu konvergují, máme tam vodorovné asymptoty, z výsledků těchto limit pak dojdeme k závěru, že přímka y = 0 je vodorovnou asymptotou v nekonečnu i v mínus nekonečnu.

Krok 3. Najdeme derivaci a použijeme ji k určení monotonie a lokálních extremů.

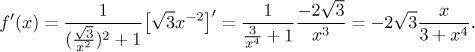
Kritické body: V definičním oboru nejsou body, kde by derivace neexistovala; derivace je nula v bodě x = 0, ale ten bod není v definičním oboru, a tak to nakonec kritický bod není. Nejsou kritické body, takže dva intervaly definičního oboru jsou také intervaly monotonie. Určíme ji pomocí tabulky.

Závěr je, že f je rostoucí na (−∞,0) a klesající na (0,∞).

Lokální extrémy: Nejsou lokální extrémy (monotonie se v bodě 0 mění, ale tento bod není v definičním oboru).

Krok 4. Najdeme druhou derivaci a použijeme ji k určení konvexity.

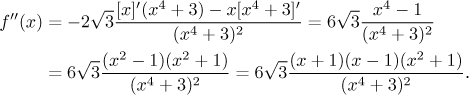
Dělící body: V definičním oboru nejsou body, kde by druhá derivace neexistovala; druhá derivace je nula pro x = −1 a x = 1. Definiční obor se tak rozdělí na čtyři intervaly konvexity, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

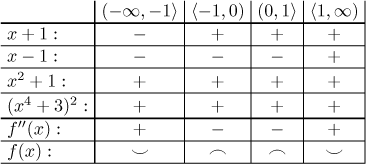
Závěr je, že f je konvexní na (−∞,−1⟩ a na ⟨1,∞); je konkávní na ⟨−1,0) a na (0,1⟩.

Inflexní body: Jsou dva, v −1 a v 1. Hodnoty jsou

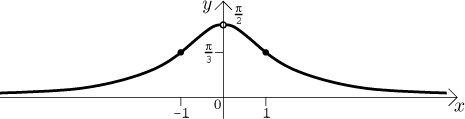
Krok 5. Teď to dáme všechno dohromady. Nejprve načrtneme do obrázku všechny body a limitní trendy, které jsme našli. To bude kostra, na kterou pak funkci pověsíme.

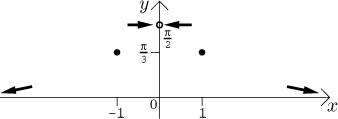
Abychom si tvar grafu lépe představili, zkombinujeme ony dvě tabulky výše.

Náčrt bude přesnější, když zjistíme, jaké jsou jednostranné limity derivace v 0 a derivace v −1 a v 1.

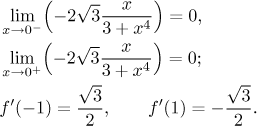
Vidíme, že se graf točí k té díře v 0, jako by tam byla vodorovná tečna (pokud bychom definici rozšířili na spojitou funkci na celé reálné ose, jak jsme diskutovali výše, pak by v bodě 0 byla vodorovná tečna a také lokální maximum). Vidíme také, že graf prochází body inflexe méně příkře než pod úhlem 45 stupňů. Teď jsme připraveni nakreslit průběh funkce.

Další příklad
Zpět na Řešené příklady - Průběh funkce