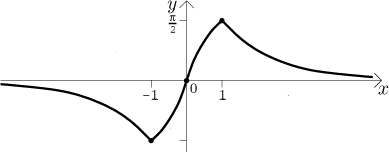
Příklad: Načrtněte průběh funkce

Řešení: Použijeme postup popsaný v sekci Přehled kreslení grafů v části Přehled metod - Průběh funkce.

Krok 1. Protože je jmenovatel zlomku vždy nejméně 1, je jediná podmínka na x vynucena arcsinem, ten vyžaduje, aby byl jeho argument mezi −1 a 1. Ukáže se, že toto vždy platí, na tuto funkce jsme se dívali už v tomto příkladě v části Řešené příklady - Derivace a zjistili tam, že definiční obor f je celá reálná osa. Všimneme si, že tato funkce je tam spojitá.

Co se dá říct o symetrii? Protože arkussinus je lichá funkce a uvnitř máme zlomek s lichým čitatelem a sudým jmenovatelem, zkušený funkční badatel by hned řekl, že f je evidentně lichá. Zkusíme to najisto, dosadíme -x do f a uvidíme, co se stane.

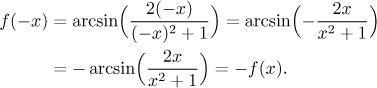
Právě jsme dokázali, že je f lichá.

Průsečík s osou x: Arcsin je nulový pouze tehdy, je-li jeho argument nula, a ten zlomek uvnitř je nula jen pro x = 0. Vidíme, že f (0) = 0 je jediný průsečík s osou x a je to také průsečík s osou y.

Krok 2. Najdeme limity v krajních bodech intervalů definičního oboru.

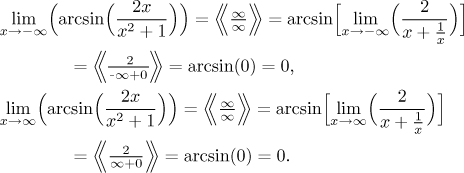
Druhou limitu jsme vlastně nemuseli počítat, protože vyplyne ze symetrie.

Asymptoty: Protože je funkce spojitá na celé reálné ose, nemůžeme mít svislé asymptoty. Protože limity v nekonečnu a mínus nekonečnu konvergují, jsou tam vodorovné asymptoty. Výsledky limit ukazují, že přímka y = 0 je vodorovná asymptota f v nekonečnu i mínus nekonečnu.

Krok 3. Najdeme derivaci a použijeme ji k určení monotonie a lokálních extremů. Najít derivaci je ale překvapivě obtížné, udělali jsme to jako samostatný příklad v části Řešené příklady - Derivace. Nakonec jsme dostali výsledek

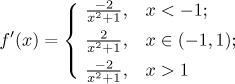
a zjistili jsme, že není derivace v bodech −1 a 1.

Kritické body: Derivace neexistuje v −1 a v 1; další kritické body jsou ty, ve kterých je derivace nula, ale takové nejsou. Máme tedy kritické body x = −1 a x = 1 a definiční obor se tak rozdělí na tři intervaly monotonie. Určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

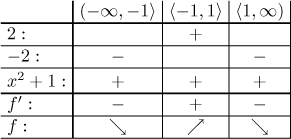
Závěr je, že f je klesající na (−∞,−1⟩ a na ⟨1,∞); je rostoucí na ⟨−1,1⟩.

Lokální extrémy: Daná funkce má lokální minimum f (−1) = −π/2 a lokální maximum f (1) = π/2.

Krok 4. Najdeme druhou derivaci a použijeme ji k určení konvexity.

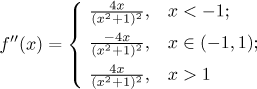
Dělící body: V definičním oboru jsou dva body, kde druhá derivace neexistuje, jmenovitě x = −1 a x = 1. Máme také bod, kde je derivace nula, x = 0. Definiční obor se tak rozdělí na čtyři intervaly konvexity, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

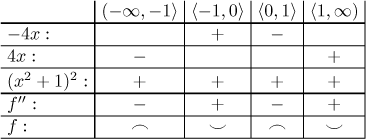
Závěr je, že f je konkávní na (−∞,−1⟩ a na ⟨0,1⟩; je konvexní na ⟨−1,0⟩ a na ⟨1,∞).

Inflexní body: f (−1) = −π/2, f (0) = 0 a f (1) = π/2.

Krok 5. Teď to dáme všechno dohromady. Nejprve načrtneme do obrázku všechny body a limitní trendy, které jsme našli. To bude kostra, na kterou pak funkci pověsíme.

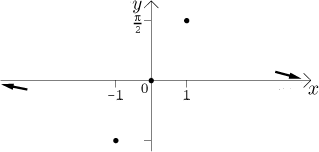
Abychom si tvar grafu lépe představili, zkombinujeme ony dvě tabulky výše.

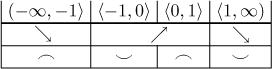
Dostaneme přesnější obrázek, když také použijeme znalost jednostranných derivací v −1 a 1.

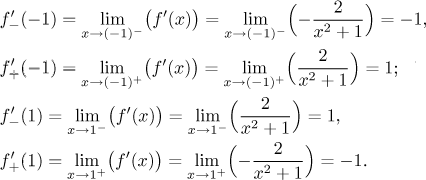
Vidíme, že v bodě −1 a v bodě 1 se křivka napojuje pod pravým úhlem. Teď jsme připraveni nakreslit průběh funkce.

Další příklad
Zpět na Řešené příklady - Průběh funkce