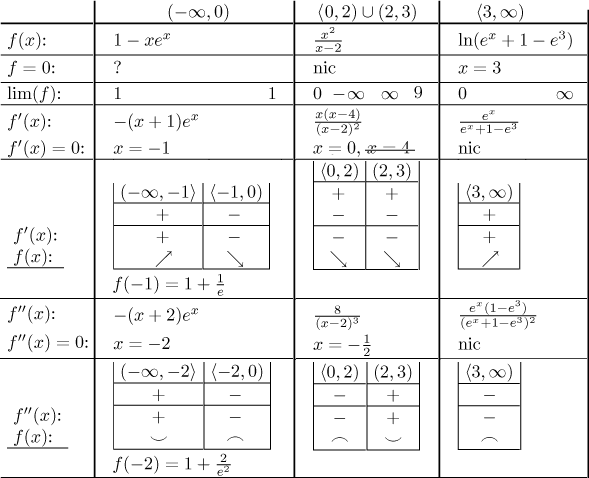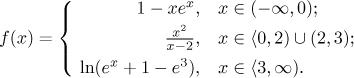
Příklad: Načrtněte průběh funkce

Řešení: Použijeme postup popsaný v sekci Přehled kreslení grafů v části Přehled metod - Průběh funkce. Jde o typickou funkci zadanou rozpisem, takže s ní budeme pracovat trochu jinak než u standardních příkladů.

Krok 1. Definiční obor u funkcí definovaných rozpisem je sjednocení všech množin z jejího popisu - tedy za předpokladu, že byla definovaná pečlivě a všechny výrazy použité při její definici opravdu existují na množinách, kde jsou použity. Protože si člověk nikdy nemůže být jistý, rychle ověříme, že každý z výrazů opravdu existuje na příslušné množině. Definiční obor je tedy

D( f ) = (−∞,2) ∪ (2,∞).

Definující výrazy jsou všechny spojité všude, kde jsou použité, takže víme, že f je spojitá na všech intervalech z definice, když je uvažujeme jako otevřené. Není ale jasné, zda je možné tyto intervaly spojit ve větší intervaly spojitosti. Vrátíme se k tomu v Kroku 2.

Co se týče symetrie, tak žádná není, protože definiční obor není symetrická množina.

Průsečík s osou x: Položíme všechny tři výrazy rovny nule. První z rovnic, které obdržíme, není možné řešit algebraicky, ale naštěstí nás zajímají jen záporná x a všimneme si, že 1 − xe^x je pro taková x vždy kladné, takže tam průsečíky nejsou. Druhý výraz je roven nule pro x = 0 a šťastnou náhodou 0 náleží do množiny, na které je tento výraz v definici použit, takže máme f (0) = 0 jako průsečík s osou x a také s osou y. Konečně třetí výraz je nula přesně pokud x = 3, což zase patří do příslušné množiny a máme druhý průsečík v 3.

Krok 2. Najdeme limity v krajních bodech intervalů z definice.

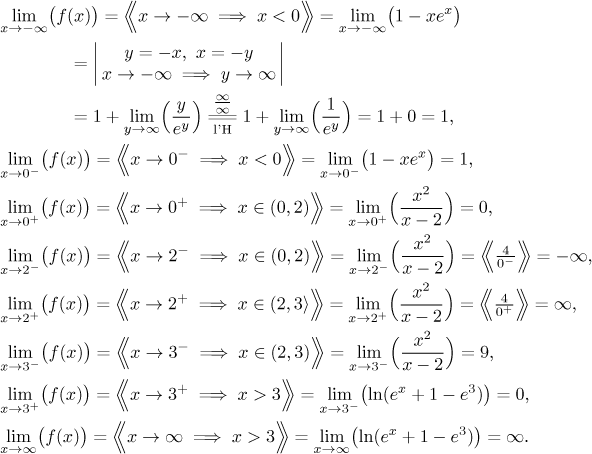
Teď už jsme připraveni rozhodnou spojitost. Uděláme tabulku, která shrne situaci ve spojovacích bodech.

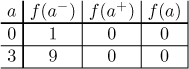
Vidíme, že limita v bodech 0 a 3 neexistuje, takže tam funkce nemůže být spojitá a nespojitosti tam nejsou odstranitelné. Na druhou stranu všechny příslušné jednostranné limity konvergují, takže máme skokové nespojitosti v bodech 0 a 3. Vidíme také, že tato funkce je spojitá zprava v 0 a spojitá zprava v 3. Kvůli těm dvěma nespojitostem nemůžeme spojit intervaly z definice ve větší intervaly spojitosti; nejlepší, co se dá říct, je že f je spojitá na všech intervalech objevujících se v její definici.

Asymptoty: Kandidáti pro svislé asymptoty jsou vlastní krajní body intervalů definičního oboru a body nespojitosti, takže kandidáti jsou 0, 2 a 3. Obě jednostranné limity v 0 konvergují, takže tam svislá asymptota není. Podobně usoudíme, že nemáme svislou asymptotu v bodě 3. V bodě 2 nicméně máme nevlastní jednostrannou limitu (dokonce obě, ale jedna stačí), takže v bodě x = 2 je svislá asymptota.

Limita v mínus nekonečnu konverguje, takže tam máme vodorovnou asymptotu, jmenovitě přímku y = 1.

Konečně v nekonečnu je limita nekonečno, takže tam není vodorovná asymptota, ale je tam šance na šikmou. Použijeme příslušný algoritmus.

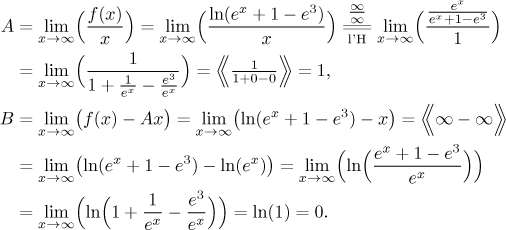
Protože obě limity konvergují, máme v nekonečnu šikmou asymptotu, je to přímka y = x.

Krok 3. Najdeme derivaci a použijeme ji k určení monotonie a lokálních extremů. Připomeňme, že derivování pomocí pravidel funguje pouze na otevřených intervalech.

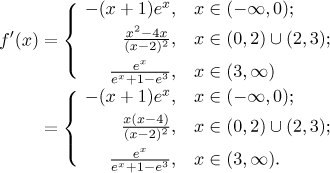
Kritické body: Protože funkce není spojitá v bodech 0 a 3, tak tam také nemá derivaci a máme první dva kritické body. Další body najdeme tak, že položíme derivaci rovnou nule.

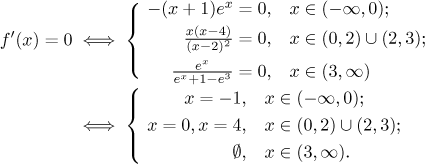
Musíme vyškrtnout řešení, která neleží v oblastech, kde příslušný vzorec dával f ′, což vylučuje 0 a 4. Máme tedy kritické body −1, 0 a 3, což rozdělí dva intervaly definičního oboru na pět intervalů monotonie, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá. Jako obvykle u funkcí zadaných rozpisem je třeba být opatrný, kde používáme různé výrazy.

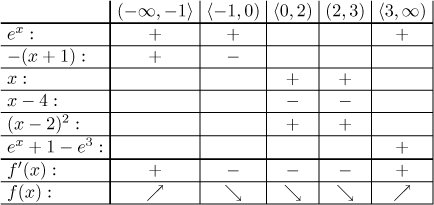
Máme sousedící intervaly stejné monotonie. Protože je v bodě 2 díra v definičním oboru, nedají se tam intervaly spojit. Máme ale šanci je napojit v nule. Mohli bychom to udělat automaticky, pokud by tam f byla spojitá, ale bohužel to není pravda. Nezbývá než použít selský rozum (viz Monotonie v části Funkce - Teorie - Reálné funkce). Víme, že f je klesající nalevo i napravo od 0, víme také, že

f (0^-) > f (0) = f (0⁺),

z čehož odvodíme, že se opravdu dají spojit intervaly monotonie v 0 (viz náčrt grafu níže). Závěr je, že f je rostoucí na (−∞,−1⟩ a na ⟨3,∞); je klesající na ⟨−1,2) a na (2,3).

Lokální extrémy: Daná funkce má lokální maximum f (−1) = 1+1/e a lokální minimum f (3) = 0.

Mimochodem, když dáme dohromady informaci o monotonii s limitami v krajních bodech spočítanými výše, vidíme, že pro x < 0 není průsečik s osou x, tj. rovnice xe^x = 1 tam nemá řešení (to byla nedokončená záležitost z Kroku 1).

Krok 4. Najdeme druhou derivaci a použijeme ji k určení konvexity. Jako v Kroku 3 pracujeme v každé oblasti zvlášť.

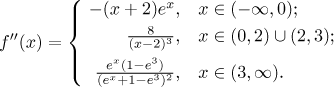
Dělící body: Druhá derivace neexistuje v bodech 0 a 3 a je nulová v bodě −2. Tyto tři body rozdělí dva intervaly definičního oboru na pět intervalů konvexity, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

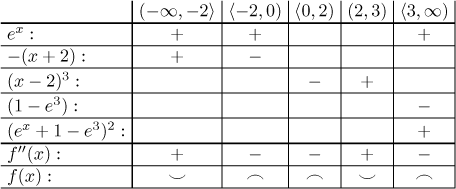
Závěr je, že f je konvexní na (−∞,−2⟩ a na (2,3); je konkávní na ⟨−2,0), na ⟨0,2) a na ⟨3,∞).

Inflexní bod: f (−2) = 1+2/e².

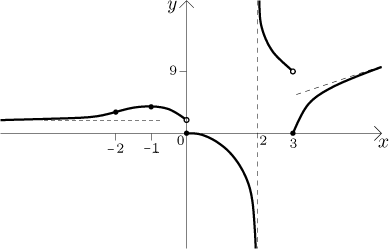
Krok 5. Teď to dáme všechno dohromady. Nejprve načrtneme do obrázku všechny body a limitní trendy, které jsme našli. To bude kostra, na kterou pak funkci pověsíme. Aby byl obrázek menší, nepoužijeme na ose y stejnou škálu jako na ose x, ale základní tvar obrázku zůstane stejný. Mimo jiné se tedy neděste, že asymptota y = x nesleduje diagonálu.

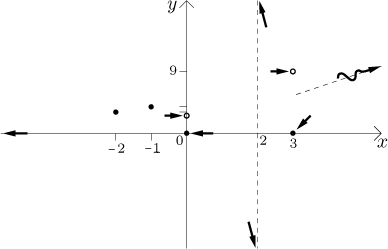
Abychom si tvar grafu lépe představili, zkombinujeme ony dvě tabulky výše.

Dostaneme přesnější obrázek, pokud najdeme limity derivace v bodech nespojitosti, abychom věděli, jakým směrem mají jednotlivé části grafu vyrazit.

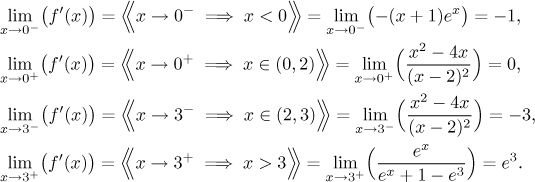
Teď jsme připraveni nakreslit průběh funkce.

Poznámka: Když pracujeme s funkcemi danými rozpisem, rozdělíme reálnou osu na několik oblastí podle její definice a pak vlastně děláme onen postup několikrát, v každé oblasti zvlášť, a v každé z nich ignorujeme výsledky, které spadají mimo dotyčnou oblast. Předchozí výpočty se dají (stručně) vyjádřit takto.

Zpět na Řešené příklady - Průběh funkce