Příklad: Vypočítejte integrál

Řešení: Tento integrál evidentně patří do šuplíku "odmocnina z kvadrátu", jmenovitě jde o typ, který se řeší substitucí A/cos(t). Protože to je většinou hodně práce, zamyslíme se stručně nad alternativami. Ostatní specializované šuplíky se nehodí, zbývá jen nějaká substituce. Jsou dva rozumní kandidáti, y = x² − 4 a y² = x² − 4. Oba budou fungovat jen tehdy, pokud se nám nějak podaří zpracovat výraz x⋅dx. V dané integrálu se nevyskytuje, jedinou nadějí tedy zůstává, pokud by se podařilo nějak algebraicky vyjádřit x pomocí y. Zkušenost říká, že to není dobrý nápad, a taky žene, výsledné výrazy jsou tak nepříjemné, že se integrál vůbec nezjednoduší. Je to tedy slepá ulička, detaily se dají najít zde.

Jediný způsob je tedy standardní přístup a my se dáme do doporučené substituce.

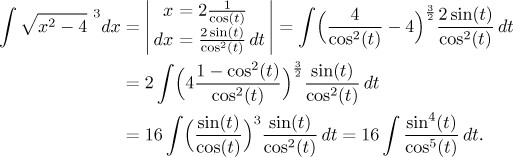
V tomto integrálu, který evidentně patří do šuplíku "goniometrické integrály". Máme jeden extra kosinus extra, což naznačuje, že sinová substituce může být dobrý nápad. Takže si ten kosinus přesuneme metodou vynásobím-vydělím do čitatele, přepíšeme zbytek jako výraz se siny a pak použijeme sinovou substituci:

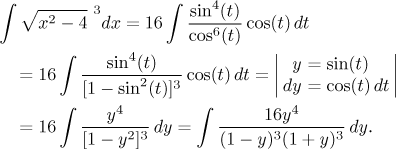
Tohle je racionální lomená funkce. Ještě se rychle přesvědčíme, že ve zlomku nejde nic pokrátit, ani jej nelze udolat substitucí (čitatel není blízký derivaci jmenovatele), a už nasazujeme parciální zlomky. Mimochodem, tu šestnáctku jsme zahrnuli do čitatele, abychom snížili šanci, že se v parciálních zlomcích objeví zlomky - výpočet je pak snažší. Máme dva lineární faktory ve vyšší mocnině, dostáváme tedy obecný rozklad

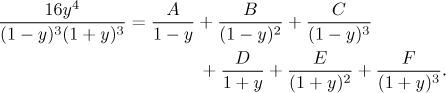
Dvě konstanty - C a E - se zdarma dostanou zakrývacím trikem, na zbývající potřebujeme čtyři rovnice. To dokáže násobící metoda, práce se dá zjednodušit pomocí triků. Protože je to rutinní výpočet, necháme jej jako poznámku. Dostaneme rozklad

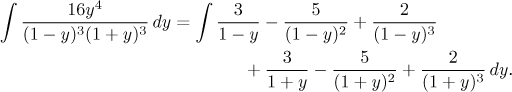
Teď integrujeme, zkušení integrátoři to dělají rovnou (ale opatrně na znaménko), ti opatrnější použijí substituce s = 1 − y a t = 1 + y. Měli byste dostat

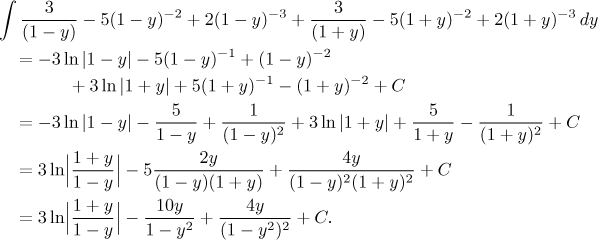
Ty poslední úpravy jsme dělali, protože teď budeme muset zpětně dosadit sinus, takže jsme si to trochu zjednodušili dopředu:

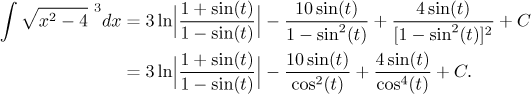
Teď nás čeká poslední zpětná substituce. Nejprve si spočítáme, kolik je sinus, uděláme přitom malý podvod s vynechanou absolutní hodnotou, jak jsme to diskutovaliv sekci o tomto šuplíku:

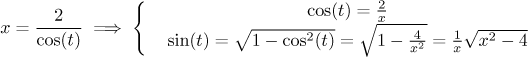
Vzorec lze také získat pomocí vhodného trojúhelníka, kde vyjdeme ze vzorce pro kosinus výše, dopočítáme třetí stranu a pak už je sinus jasný.

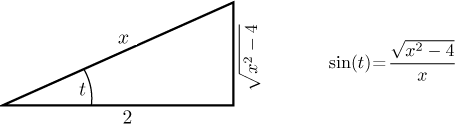
Konečně dostáváme

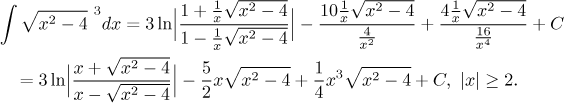
Po tak dlouhém výpočtu (a malém podvodu) je zkouška opravdu nutností, zejména že nenastane problém se zápornými x. Derivování ukáže, že je vše v pořádku.

V šuplíku "odmocniny z kvadrátu" jsme se zmínili o alternativní metodě, jmenovitě o Eulerových substitucích. Můžeme použít hned tu první a dostaneme:

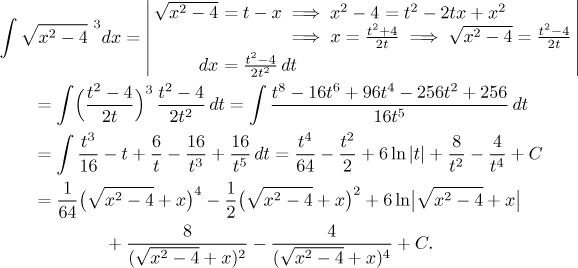
Výpočet byl překvapivě relativně snadný, ale odpověď vypadá dost drsně. Je vůbec stejná jako náš první výsledek? Vlastně ano, ale ukázat to není zrovna snadné, viz tato poznámka.

Protože výraz pod odmocninou lze rozložit, máme také k dispozici dvě verze 3. Eulerovy substituce:

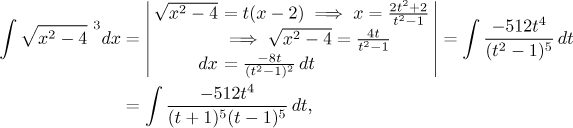
popřípadě

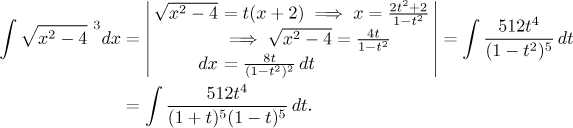
Tento postup skončil s integrály podobnými našemu prvnímu postupu, ale ve jmenovateli jsou teď vyšší mocniny, takže by rozklad na parciální zlomky vyžadoval osm rovnic, nic příjemného. Tohle není dobrý nápad.

Další alternativní řešení, které bylo v šuplíku zmíněno, je hyperbolická substituce:

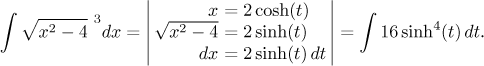
Integrály z hyperbolických funkcí jsme zmínili v šuplíku "goniometrické integrály" a doporučovali jsme postupovat podobně jako u integrálů goniometrických. V tomto konkrétním případě se nabízí redukční vzorce, které lze odvodit nebo najít v tabulkách. Protože zrovna nemáme tabulky po ruce, použijeme metodu další: metodu snížení mocniny pomocí identit, které jsou pro hyperbolické funkce trochu odlišné ale velice podobné těm goniometrickým. Násobky argumentu pak řešíme linární substitucí:

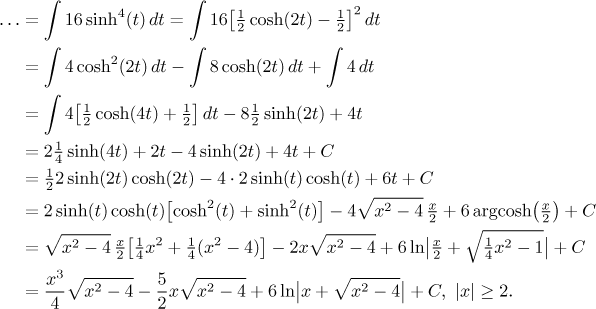
Tento výsledek se dá relativně jednoduše přepsat, aby souhlasil s naším prvním výsledkem, stačí upravit ten logaritmický člen, což jsme již dělali v této poznámce.

Další příklad
Zpět na Řešené příklady - Integrace