Nevlastní integrály: Přehled metod

První, co by si měl člověk zapamatovat, je, že libovolný určitý integrál vlastně může být nevlastní integrál - ne vždy je to jasné na první pohled. Kdykoliv máme spočítat určitý integrál, musíme prozkoumat integrační interval, jestli se tam nevyskytují problémy. Ty jsou dvojího druhu:

• jedna či obě integrační meze (koncové body integračního intervalu) jsou nekonečné;
• integrovaná funkce není spojitá v některých bodech integračního intervalu; nejčastěji je v tom zamícháno dělení nulou.

Pokud problémy nejsou, pak lze integrál přímo spočítat, nejpravděpodobněji asi pomocí primitivní funkce (viz Výpočet určitého integrálu v části Přehled metod).

Pokud se problémy vyskytnou, musíme si pamatovat, že umíme bezpečně spočítat pouze nevlastní integrály, které mají právě jeden problém, a to v jednom z koncových bodů. Pokud máme problémů více, musíme rozdělit integrační interval na menší intervaly, aby každý z nich obsahoval nejvýše jeden problém (a to na konci). Aby celý integrál konvergoval, musí konvergovat všechny jeho menší části.

Stačí tedy znát, jak se vypořádat se dvěma základními typy nevlastního integrálu: ty s problémem u horní meze a ty s problémem u dolní meze. Jsou také dvě základní otázky ohledně takových integrálů: výpočet a rozhodnutí, zda konvergují.

Výpočet nevlastních integrálů

Otázka je jednoduchá: Vypočítejte (pokud konverguje)

Řešení je založeno na definici nevlastního integrálu.

Pokud je problém na pravém konci b - typicky bychom také požadovali, ať je f spojitá na ⟨a,b) - odřízneme problém takto:

Pokud je problém na levém konci a - typicky bychom také požadovali, ať je f spojitá na (a,b⟩ - odřízneme problém takto:

Integrál konverguje, pokud konverguje limita, pak dostaneme odpověď. Jinak nevlastní integrál diverguje (ale někdy má pořád ještě smysl přiřadit odpověď, nekonečno či mínus nekonečno).

Při praktickém výpočtu počítáme limitu v problémovém bodě až nakonec, po vyhodnocení neurčitého integrálu. Jinými slovy, s oběma integračními mezemi, problémovou i tu druhou, zacházíme jako obvykle, včetně změny mezí v substituci, pokud je to třeba, a až ve chvíli dosazení (popř. při změně v substituci) použijeme u problémové meze limitu.

Když se počítá ta limita, je důležité ji aplikovat na celou primitivní funkci, nerozdělovat ji na několik částí, pokud si nejsme zcela jisti, že to nezpůsobí potíže. Jinými slovy, kdykoliv je to možné, vyjádřete primitivní funkci jako jeden výraz a ne součet více výrazů.

Příklad

Testování konvergence nevlastních integrálů

Otázka je jednoduchá: Rozhodněte, zda tento integrál konverguje:

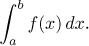
Existují v zásadě tři způsoby, jak najít odpověď.

1. Vypočítejte integrál. To se přirozeně dělá jen v případě, kdy je to velmi snadné, nebo když ostatní metody selžou.

2. Použijte Srovnávací kritérium.

Protože závěr testu není ve formě ekvivalence, je to "jednosměrný" test a funguje jen někdy - jmenovitě pokud nám nerovnost mezi f a testovací funkcí dovoluje odvodit něco o jejich integrálech. Někdy je jediným možným závěrem konstatování, že žádný závěr není možný. Jsou jen dva případy, kdy je Srovnávací kritérium úspěšné:

• Pokud si myslíme, že daný integrál s f konverguje, snažíme se najít nějakou větší testovací funkci g tak, aby její integrál také konvergoval. Zde ovšem musíme být trochu opatrní, protože aby byl test platný, musíme také najít dolní odhad pro f. Buď zjistíme, že f je vždy nezáporné (což je standardní verze Srovnávacího kritéria), nebo použijeme g k majorizaci nejen samotného f, ale absolutní hodnoty f (verze Srovnávacího kritéria s absolutní hodnotou).
• Pokud si myslíme, že daný integrál s f diverguje, snažíme se najít nějakou menší testovací funkci h tak, aby její integrál také divergoval. V tom případě navíc potřebujeme, aby byla funkce h všude nezáporná.

3. Použijte Limitní srovnávací kritérium.

Nejprve najděte testovací funkci g, která je (až na nenulový násobek) v zásadě stejná jako f pro x blízké problémovému bodu. Pak je třeba ověřit správnost testovací funkce tím, že se spočítá limita podílu f /g pro x blížící se k problémovému bodu (z příslušné strany). Tato limita by měla existovat a být nenulová. Pokud se tak stane, tak následně rozhodněte, zda konverguje integrál z g od a do b. Tento závěr se pak také vztahuje na daný integrál.

Jak najít tu "správnou" testovací funkci:

Vše vychází z toho, že se podíváme na výraz definující f a zkusíme ignorovat všechny části, o kterých si myslíme, že nejsou důležité, když je x blízko k problémovému bodu. Pokud to uděláme dobře, měli bychom dostat testovací funkci, která je jednodušší, podobná funkci f poblíž problémového bodu (což nám umožní použít Limitní srovnávací kritérium) a při troše štěstí je dokonce všude větší (popřípadě všude menší) než f, což by nám umožnilo použít jednodušší Srovnávací kritérium - pak bychom ovšem ještě museli mít i štěstí, abychom dostali nějaký závěr, tj. aby ta nerovnost šla správným směrem.

Protože tento postup nejčastěji vede k mocnině (či přesněji řečeno k reciproké mocnině), je důležité si pamatovat srovnávací škálu mocnin v nekonečnu a v nule - viz Teorie - Nevlastní integrály - Vlastnosti a příklady.

Tento proces se zdá být snadnějším v případě nekonečné integrální meze. Předpokládejme například, že v našem integrálu je b = ∞. Pak se podíváme na všechny součty ve výrazu pro f a v každém z nich si ponecháme jen dominantní člen. Díky zkušenostmi s limitami víme, že když je x blízko nekonečnu, tak exponenciály porazí mocniny, ty zase porazí mocniny logaritmu. Když se rozhoduje mezi mocninami, vždy vyhraje ta vyšší. V typickém případě máme zlomek, pak vybereme dominantní členy čitatele a jmenovatele a máme tu nejlepší testovací funkci.

Pokud je problém způsoben nespojitostí, může to být obtížnější a je třeba aplikovat odlišnou metodu. V typickém případě máme zlomek, jehož jmenovatel je v problémovém bodě roven nule. V tomto případě bychom postupovali jinak než v předchozím případě. Zatímco u nekonečna ignorujeme "nedůležité členy" v součtech, zde bychom ignorovali nedůležité části součinů. Přesně řečeno, vyjádřili bychom si f jako součin co nejjednodušších členů (některé z nich mohou být ve jmenovateli) a pak si ponecháme pouze ty z nich, které jsou v problémovém bodě rovny nule. Dalším populárním nástrojem je Taylorův rozvoj se středem v problémovém bodě, díky čemuž můžeme nahradit nepříjemné funkce polynomem.

Příklad

Příklad