Příklad: Určete, zda následující řada konverguje.
![]()
Řešení: Členy této řady jsou kladné, takže můžeme použít všechny ty
báječné testy, ale možná je lepší začít bližším pohledem na ty členy.
Vidíme, že
Pro řady s mocninami často používáme podílové kritérium. Jak příslušný podíl vypadá?
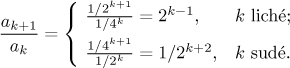
Když k roste do nekonečna, tak liché zlomky utíkají do nekonečna,
zatímco sudé jdou k nule. To ukazuje, že limita pro
λ neexistuje a podílové
kritérium ve své limitní verzi nefunguje. Ono dvojí chování ukazuje, že ani
obecnější verze podílového kriéria (ty s nerovnostmi) nebudou fungovat,
protože nedokážeme přinutit podíl
Což takhle odmocninové kritérium?
![]()
Stejně jako u podílového kritéria, limita pro
ϱ neexistuje a tudíž limitní verze odmocninového testu nefunguje.
Zde ale máme šanci použít obecnou verzi s nerovnostmi. Jestliže totiž
vezmeme
![]()
To dokazuje, že daná řada konverguje.
Alternativa: Můžeme také zkusit použít srovnání. Díky schizofrenní podstatě této řady nemůžeme doufat, že by se její členy podobaly nějaké věci pro velká k, čímž se vylučuje limitní srovnávací kritérium, ale máme tu pěknou příležitost použít to obyčejné srovnávací kritérium. Máme
![]()
Protože řada napravo konverguje
(je to geometrická řada
s
Alternativa: Je ještě jeden zajímavý trik, který by se dal zkusit.
Daná řada má členy dvou typů, proto je můžeme rozdělit do dvou samostatných
řad. Vyjádříme ji tedy jako součet
![]()
Co se dá říct o konvergenci těchto dvou řad? Na první pohled jsme si moc nepomohli, zase jsou obě takové dvojité, jenže - a to je právě ta finta - nuly se dají z řady bez problémů vypustit. Řady je tedy možno přepsat pomocí obvyklých výrazů pro sudá a lichá čísla následovně.
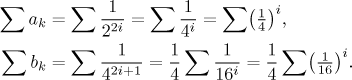
Vidíme, že v obou případech jde o
geometrickou řadu, obě mají
Další příklad
Zpět na Řešené příklady -
Testování konvergence