Sequences of functions

We start with a definition of a sequence of functions and dedicate most of this section to investigating convergence, above all to the problem of preservation of properties. Eventually we will have no choice but to introduce uniform convergence. At the end we briefly look at monotonicity.

Definition.
By a sequence of functions we mean any countable ordered set

{ f_k}_{k ≥ n0} = { f_n0,  f_n0+1,  f_n0+2,...},

where f_k are functions and the starting index n₀ is some integer.

Depending on what kind of functions we consider, we get different theories. Here we will only consider real functions, that is, functions defined on subsets of real numbers and with real values. Another popular option is complex functions and in fact most results from here can be transferred with minor (and usually obvious) modifications to the complex case, but that is beyond the scope of Math Tutor.

Our main interest now is developing the notion of convergence for sequences of functions, in which case we do not really care about the beginning of the given sequence. Then - as usual - we will simplify our life by simply writing { f_k}.

If we want to study sequences of functions, a good start is to imagine their graphs. We have one picture with coordinate axes and we draw infinitely many graphs into this picture. If any reasonable work is to be done, we need to have at least a little place on the real line where all of these functions actually exist. That is, the whole work in this and subsequent sections is based on the usually unspoken assumption that the domains of all f_k have non-empty intersection. We then work on this intersection and essentially disregard anything that happens outside this common set. So the right idea at the start is to imagine a nice set on a real line (perhaps an interval) and infinitely many functions (graphs) on it.

Before we get to the main definition, we will try to figure out what makes actually sense. The most natural approach to sequences of any kind is to fall back on what we know - sequences of (real) numbers. Given a sequence of functions { f_k}, we can choose a certain number x from the intersection of their domains and substitute it into all of these functions. Every f_k(x) is then a number, thus we obtain a sequence { f_k(x)} of real numbers. We know how to deal with these; in particular we can inquire whether this sequence is convergent or not. If it is, then we get some limit A - a real number.

When we try this for all numbers x from the intersection of domains, we see that this intersection splits into two parts. For some x the resulting real sequence does not converge. For some it does, these form the region of convergence for the given sequence of functions. For each x from this region we get the appropriate limit A of { f_k(x)}, we should actually write something like A_x as the value of the limit obviously depends on the choice of x. What is the situation now? We were given a reasonable sequence of functions (whose domains have non-empty intersection) and we identified a region of convergence. It may be empty, but if it is not, then we have a certain subset of real numbers and for every x from this set we have a value assigned, namely the limit A_x. In other words, we have a new function, call it f. If we want to know how much is f (x), we take this x and find the limit of { f_k(x)}. This function f is naturally called the limit of the sequence { f_k}. We are ready for a formal definition and some nice examples.

Definition.
Consider a sequence of functions { f_k}.
We define its region of convergence as the set of all x for which all f_k are defined and the sequence { f_k(x)} converges.
On this region of convergence we define the function f called the limit of { f_k} by the formula

Since the main focus now is functions, not numbers (that is, we prefer to talk on the level of functions as abstract objects), we would like a notation that would not refer to points. The fact that a function f is the limit of a sequence of functions { f_k} is denoted by

However, we know that when dealing with functions it is crucial to know where they live and where things work, which we do not see from the "lim" notation. There is no widely accepted notation for the region of convergence, in particular because we sometimes choose to work on smaller sets anyway. Therefore we introduce the following more general convention. If M is any subset of the region of convergence (for instance the region itself), then we say that the sequence { f_k} converges to f on M. Often we prefer to refer to functions themselves rather than to the sequence they form, so people also say that functions f_k converge to f on M. Both statements can be written as

f_k→f on M.

We will shortly see that there are other ways to look at convergence of functions. It is generally accepted that when we talk about convergence without further specification, we mean the one we just defined, in particular because it is the basic one, other kinds of convergence usually work by adding some conditions to this notion that we already have. However, sometimes we want to emphasize that we indeed mean this convergence, that we indeed look at what is happening at individual points. Then we would say that f_k converge pointwise to f on M.

Remark: When dealing with sequences of real numbers, we were also interested in a particular case of divergence, when the limit was infinite. Here this is of no interest, since the right kind of object to obtain as a limit of a sequence of functions is a function again, and we cannot assign the value infinity to a function.

Example: Consider the sequence given by f_k(x) = x^k for k = 1,2,3,...

All these functions are defined on the whole real line, so the set of real numbers is our starting position for the investigation of the sequence of functions {x^k}. When we fix an arbitrary real number, it becomes a constant, thus the sequence {x^k} turns into a geometric sequence. Indeed, if we take for instance x = 2, then we get the sequence {2^k}. If we take x = −1/2, then we get the sequence {(−1/2)^k} etc. We know very well how such a geometric sequence behaves, its convergence depends on its base, the number x that we fix. Therefore we know that if |x| < 1, then {x^k} converges to 0, and if x = 1, then {x^k} = {1^k} = {1} converges to 1. We also know that all other choices of x give divergent geometric sequences. Thus we have the following conclusion:

The region of convergence of the given sequence is the interval (−1,1] and on this interval we have

If we call the resulting function f, then we can also write that x^k→f on (−1,1]. The following picture suggests what is happening, we draw the first five functions of the given sequence. On the left we look at a large part of the real line, but the functions run away too fast to help us with the really interesting region near the origin, so we focus on it in the picture on the right and show some more powers (up to x¹⁰ to be precise).

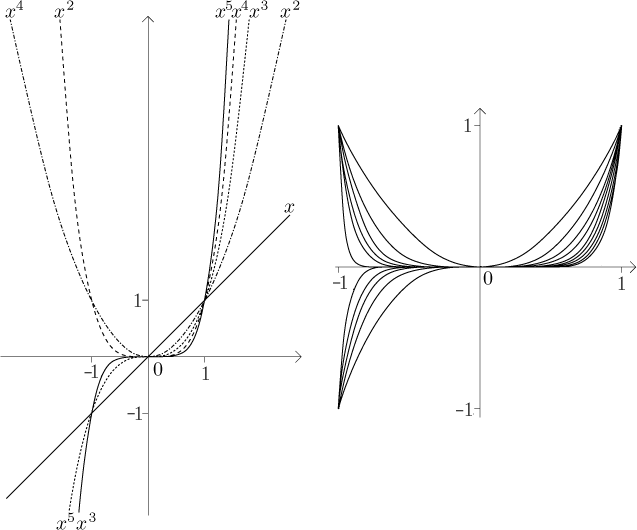
We see that the graphs of x^k on (−1,1) as curves approach the x-axis, that is, to the function 0 (if you want to see an animation, click here). We will return to this example below.

Example: Consider the sequence given by f_k(x) = arctan(k⋅x) for k = 1,2,3,...

All these functions are defined on the whole real line, so the set of real numbers is our starting position for the investigation of the sequence of functions {arctan(kx)}. When we fix an arbitrary real number, then for positive x the sequence {kx} goes to infinity as k goes to infinity and arctangent is equal to π/2 there. If x is negative, then {kx} goes to minus infinity and arctangent is equal to -π/2 there. If x = 0, then after substituting it into the sequence {arctan(kx)} it becomes the sequence {0} that converges to 0. We therefore have

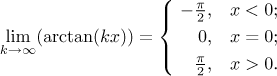
Again, a picture shows what is happening.

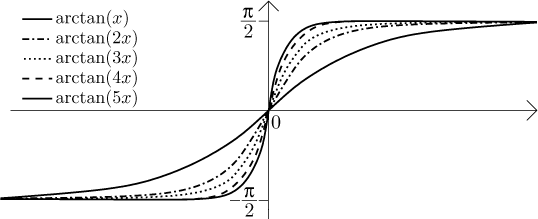
With growing k the curves (graphs) approach more and more constant functions -π/2 and π/2.

Since the notion of convergence for functions is derived from convergence of real numbers, many nice properties are preserved. First of all, convergence of functions behaves well with respect to the usual algebraic operations.

Theorem.
Assume that a sequence of functions { f_k} converges to a function f on a set M and that a sequence of functions {g_k} converges to g on the same set M. Then the following is true:
(i)  For any real number a, the sequence {a⋅ f_k} converges to a⋅ f on M.
(ii)  The sequence { f_k + g_k} converges to f + g on M.
(iii)  The sequence { f_k − g_k} converges to f − g on M.
(iv)  The sequence { f_k⋅g_k} converges to f⋅g on M.
(v)  The sequence { f_k/g_k} converges to f/g on the set of all x from M for which all g_k(x) are not 0.
(vi)  The sequence { f_k^g_k} converges to f ^g on the set of all x from M for which all f_k(x) are positive.

In short, operations work whenever and wherever the outcome makes sense (for the last condition recall how we treat general powers). Note that the first two statements together combine into the statement that the notion of limit satisfies linearity.

Composition is tricky. Limit works well with composition of functions only under some special conditions, see for instance the corresponding theorem in the section Basic properties in Sequences - Theory - Limit. Therefore we will not offer any general statement that would say something along the lines that f_k(g_k) should converge to f (g), this fails even for continuous functions. If we want to do something like this, then we have two options. Either we make the convergence better, that is something that will come later. The other way is to make the situation less general and work with just one sequence.

Theorem.
(i)  Assume that a sequence of functions { f_k} converges to a function f on a set M and that a function g maps N into M. Then the sequence { f_k(g)} converges to f (g) on N.
(ii)  Assume that a sequence of functions {g_k} converges to a function g on a set N, a function f is continuous on M and all g_k map N into M. Then the sequence { f (g_k)} converges to f (g) on N.

Some properties of functions are preserved by convergence.

Theorem.
Assume that a sequence of functions { f_k} converges to a function f on a set M.
(i)  If all f_k are odd, then also f is odd.
(ii)  If all f_k are even, then also f is even.
(iii)  If all f_k are T-periodic, then also f is T-periodic.
(iv)  If all f_k are non-decreasing functions, then also f is a non-decreasing function.
(v)  If all f_k are non-increasing functions, then also f is a non-increasing function.
(vi)  If all f_k are constant functions, then also f is a constant function.

The last statement invites a clarifying remark. We talk of a sequence of constants there. Every function as individual is a constant, but each may be different. On the other hand, a constant sequence of functions is a sequence where all functions are the same, but not necessarily constant functions, For instance, if f_k(x) = x² for all k, then we obtain a constant sequence, and it obviously converges to x². In general a constant sequence converges to that constant element - just like in the case of real sequences.

We observed (see Functions - Theory - Limit and comparison) that passing to a limit may change inequality into equality, but never into an opposite inequality. This explains why in (iv) and (v) above monotonicity survives, but strict monotonicity does not, see below.

We saw some properties that are preserved, but unfortunately the really interesting properties cannot be relied on to survive convergence. In particular:
(1) even if all  f_k are 1-1,  f need not be 1-1;
(2) even if all  f_k are increasing,  f need not be increasing;
(3) even if all  f_k are decreasing,  f need not be decreasing;
(4) even if all  f_k are bounded,  f need not be bounded;
(5) even if all  f_k are continuous,  f need not be continuous;
(6) even if all  f_k are differentiable,  f need not have derivative;
(7) even if all  f_k are integrable,  f need not be integrable.

Indeed, all those arctangents in the last example are increasing, 1-1, continuous, and they have derivatives of all orders everywhere, but the limit is not even continuous at 0, to say nothing of derivatives there, and it fails strict monotonicity and 1-1 about as much as a function can. As continuous functions, these arctangents are also integrable and have antiderivatives on the real line, but the limit f does not have an antiderivative around the origin due to that jump.

To see that boundedness need not survive, consider this example: If we define f_k(x) = min(e^x,k), we get a sequence of bounded functions. Every function is simply the exponential that is cut off once it crosses level k and replaced by a constant there. Thus they are all bounded, but this sequence obviously converges to e^x on the real line and this is not bounded.

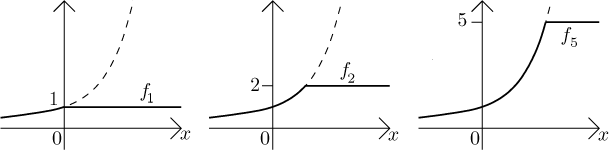
Is there any way to salvage this unpleasant situation? There are no reasonable conditions that would make (1)--(3) work. The other four can be fixed if we demand that the convergence be "better" (see the next part below). Actually, one can also fix (4) by requiring that the given sequence of functions is "uniformly bounded" and (5) by requiring that the given functions are "equicontinuous", but this is advanced stuff and we will not explore it here (it is also used much less that the "better convergence" that we do show here).

Before we get to this new convergence, we will look closer at the last three problems (5)--(7). We will show that they in fact represent the idea of "switching operations". With continuity it goes like this. The most practical way of determining continuity is via limit (see Continuity in Functions - Theory - Real functions). Consider a sequence { f_k} of continuous functions converging to some f. Let a be some point in the interior of the region of convergence. The function f is continuous there exactly if its value at a is the same as its limit at a. We will now look at this condition closer, in the last step we use the assumption that f_k are continuous.

Given a sequence of functions { f_k}, there are two things that we can move about - the index k and the variable x. In a perfect world, when we decide to apply limit to both these quantities, the order would not matter. However, we see that interchangeability of limits is equivalent to preservation of continuity and that we know is not true. Indeed, we can use the above example with arctangent to nicely illustrate that the order in which we apply the limit does matter.

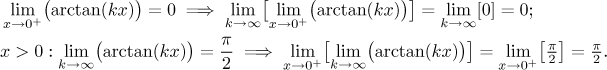
This problem appears in many situations when we can apply limit to more objects, for instance with functions of more variables, so the problem if interchangeability of limits is quite important. It is definitely worth asking under which conditions we can do it.

The derivative problem, as stated in the above list, is not exactly of this kind, but in fact we usually want more than is written there. If we have differentiable functions f_k that converge to some f on a set M, we would like to know that f is differentiable and its derivative f ′ can be obtained by taking the limit of derivatives f_k′. That is, we want to have a choice whether we first take the limit and then differentiate or the other way around.

This interchangeability of limit and differentiation is quite a problem as well. The above example with arctangent shows that we can lose differentiability entirely, but it can also happen that f does have a derivative, but we cannot reach it using  f_k, see for instance this problem in Solved Problems - Series of functions.

This brings us to the integral problem. There it is even more complicated. If integrable functions f_k converge to f on some M, then we cannot hope that antiderivatives F_k would go to F for the simple and fundamental reason that every function has infinitely many antiderivatives; we may choose one for each function, but then most likely they will not form a convergent sequence as the shifts will play hell with convergence.

There are two reasonable ways out. One is to use definite integral, so one can for instance require that on any segment between a and b that lies entirely in M,

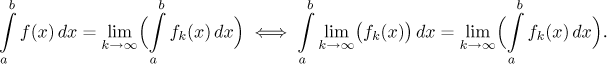
Thus we again in fact want to be able to change the order of two operations, limit and (definite) integration. The other option is to use the definite integral from some fixed a to a variable x, thus obtaining one specific choice of antiderivative, which makes good sense if the region of convergence is an interval.

Also here it may happen that f is integrable, but this integral has nothing to do with integrals of f_k. Consider the following functions.

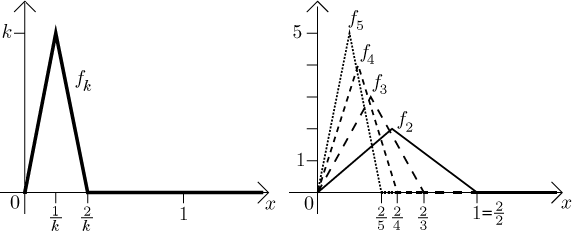
Note that as we go through this sequence, the triangles keep sliding toward 0. Thus if we fix some positive x, sooner or later those hills pass it and f_k(x) start being 0, so f_k converge to 0 for x > 0. At x = 0 they simply are all zero. This proves that { f_k(x)} converges to f = 0 on [0,∞). Now focus on the interval [0,1]. All functions involved are continuous and therefore they are integrable there, but integral over [0,1] of f is 0, while all f_k have integral 1 there. Thus integral of f cannot be obtained as a limit of integrals of f_k.

We have shown that the last three problems (5)--(7) are related to the problem of interchanging the order of limits, differentiation and integration. Now we will get some positive results about it.

Before we show its definition, we will show why it is the right one. When we lost continuity and more in the first two examples, the real cause was in different speeds of convergence. For instance, we know that for |x| < 1 the sequence x^k goes to 0, but for different x it goes there with different speeds; the closer x is to 1 (or −1), the longer it takes for x^k to get to 0. After all, the pictures above show it quite clearly. The same thing is true for the second example, the closer to zero we look, the longer those arctangents take to get to their limit.

There is another way to express this. One possible interpretation of limit is through approximation. If numbers a_k converge to A, then for every tolerance ε there is some a_K that approximates A up to that ε. Does it work for functions? The first two examples show that convergence as we defined it does not work like this. For instance, the functions x^k converge to the function 0 on (0,1), but when we choose, say, ε = 1/2, then there is no index K such that x^K would be 0 up to 1/2, every power jumps too high near 1. Thus the pointwise convergence is nice, but not quite what we expect. A better convergence is needed.

The basic idea of uniform convergence is to fix the above flaw. It allows the limit function f to be approximated arbitrarily well by a certain f_k, or equivalently, it forces f_k to converge to f everywhere at the same speed. The idea is simple: Instead of playing the limit game separately at every point, it is played simultaneously on the whole set of convergence.

Definition.
Consider a sequence of functions { f_k}. Let M be a set on which all f_k are defined.
We say that the sequence { f_k} converges to f uniformly on M if and only if for every ε > 0 there is an integer N such that for every k ≥ N and for every x from M:

| f_k(x) − f (x)| < ε.

We denote it f_k ⇉ f on M.

We start with a simple observation:

Fact.
Consider a sequence of functions { f_k} and a function f.
If f_k ⇉ f on M, then f_k→f on M.

This shows that uniform convergence is indeed stronger than pointwise convergence and we will show below that it is strong enough to do what we want from it. It also shows that attempting to establish uniform convergence makes sense only on subsets of the region of convergence of { f_k}. Finally, it shows the way to determine uniform convergence. Doing it by definition is not practical and the first of many problems is where to get that mysterious f. This Fact shows that we simply take the f from pointwise convergence, which is something that we can usually handle well. To avoid the unpleasant epsilon-delta game we then turn to another observation.

Fact.
Consider a sequence of functions { f_k} and a function f. Let M be some subset of the region of convergence of { f_k}.
Then f_k ⇉ f on M if and only if the numbers  sup_M| f_k − f |  converge to 0 as k goes to infinity.

This is in fact nothing deep, just a slightly different way of writing the definition; the supremum tells us how good a particular approximation of f by some f_k is globally on the set M, and we want this approximation to get as good as we need. Since the supremum can be often evaluated (or at least estimated), this is very practical. We get f from pointwise convergence and finding supremum of a function is also a standard problem.

Example: Consider the sequence given by  f_k(x) = x^k. We have shown that it converges to the constant function 0 on M = (−1,1), but observations that we did above strongly suggest that this convergence is not uniform. Now we prove it: For every k we obtain

sup_M| f_k(x) − f (x)| = sup{|x^k|; −1 < x < 1} = 1.

We see that quality of approximations (or speed of convergence) gets really bad near 1 and −1, so the way to get uniform convergence is to cut away these points. Take an arbitrary positive number a < 1, it is good to imagine that it is close to 1. Consider the set M = [−a,a]. For every x from this set we have |x^k| ≤ a^k, therefore now

sup_M| f_k(x) − f (x)| = sup{|x^k|; −a ≤ x ≤ a} = a^k→0.

In the last step (when evaluating the limit) we used the fact that |a| < 1. We have just proved that x^k converges uniformly to 0 on all intervals [−a,a] with a < 1. This proves what we just guessed before. The problem with convergence on the interval (−1,1) is at 1 and at −1, the closer we get, the worse the convergence. Once we cut off those ends, even if we cut off a very tiny piece (a can be arbitrarily close to 1), then situation improves dramatically. This is in fact rather typical, a reasonable series has troubles with convergence at the endpoints of its region of convergence (after all, convergence "ends" there, and it is hardly natural that it would stop abruptly, in a typical case it is getting steadily worse until it fails completely). When we cut off these endpoints, convergence becomes uniform. This behavior can be observed in many solved problems on this topic, see Solved Problems - Series of functions. Some sequences are even better, they converge uniformly everywhere, again see Solved Problems.

Similarly we easily show that in the example with sliding triangles above the convergence is not uniform on [0,∞), due to the rising triangles the relevant supremum actually goes to infinity, but once we cut off the beginning by considering [a,∞) for any a > 0, we already get uniform convergence.

Uniform convergence is markedly better than pointwise convergence. For instance, recall that we had troubles with composition. With uniform convergence we do not have to worry.

Theorem.
Assume that a sequence of functions { f_k} converges uniformly to some continuous function f on a set M and that a sequence of functions {g_k} converges to a function g on a set N. Assume also that all g_k map N into M. Then the sequence { f_k(g_k)} converges to f (g) on N.

Now we look at the properties discussed above.

The fact that (iii) is so complicated shows that derivatives can be quite tricky, even uniform convergence of f_k is not enough to get something reasonable and one has to ask things about derivatives. Then it is just an application of a certain special version of (ii). Since this version is of some independent interest, we state it here.

Proposition.
Consider a sequence of functions { f_k} that converges uniformly to a function f on some interval M. Assume that all f_k are continuous on M. Fix some a from M and for all x from M define

Then F_k converge uniformly to F on M.

We know (see e.g. the Fundamental theorem of Calculus in Integrals - Theory - Introduction) that those F_k are antiderivatives of f_k and F is an antiderivative of f. Thus we see that uniform convergence of continuous (therefore integrable) functions guarantees convergence of their integrals and we had to take special antiderivatives to avoid trouble with arbitrary constants, see discussion above.

We also have a special local version of (i) that is sometimes useful.

Proposition.
Consider a sequence of functions { f_k} defined on some neighborhood of a point a. Assume that for every k, lim_x→a( f_k(x)) = A_k for some real number A_k.
If f_k converge uniformly to some function f on some neighborhood of a, then {A_k} is a convergent sequence and lim_x→a( f (x)) = lim(A_k).

In short both (i) and this Proposition say that uniform convergence allows for changing the order of limits as we discussed above. Similarly, (ii) and (iii) state that under appropriate assumptions (uniform convergence at the right place) we can change the order of limit and integration, or limit and derivative.

Given a sequence of functions { f_k}, we can ask about monotonicity. Not surprisingly, it is done pointwise.

Definition.
Consider a sequence of functions { f_k}, let M be some set on which all f_k are defined.
(1) We say that this sequence is increasing on M if for every x from M the sequence { f_k(x)} is increasing.
(2) We say that this sequence is non-decreasing on M if for every x from M the sequence { f_k(x)} is non-decreasing.
(3) We say that this sequence is decreasing on M if for every x from M the sequence { f_k(x)} is decreasing.
(4) We say that this sequence is non-increasing on M if for every x from M the sequence { f_k(x)} is non-increasing.
We say that this sequence is monotone on M if it satisfies one of the above properties.
We say that this sequence is strictly monotone on M if it is increasing on M or decreasing on M.

In fact, here it is not necessary to do it pointwise, we can do just with functions as objects, since in Functions - Theory - Real function - Operations with functions we defined comparison (inequality) for functions on sets. Thus the sequence { f_k} is increasing on M if f_k+1 > f_k on M for every k, similarly we can define the other properties. It is actually the same, those inequalities were defined via points anyway, but in this way we hide it.

As an example we take the sequence in our first example (those powers). It is decreasing on (0,1) and increasing on (1,∞). However, this sequence is not monotone on (0,∞) since mutual relationship of these functions (direction of inequality) is just the opposite on the two parts of this set.

Uniform convergence is studied preferably on closed sets, because many things work better there (note that we also preferred statements with closed intervals above). In particular, on a closed interval one has the following interesting statement.

Series of functions
Back to Theory - Series of functions