Příklad: Načrtněte průběh funkce

Řešení: Použijeme postup popsaný v sekci Přehled kreslení grafů v části Přehled metod - Průběh funkce.

Krok 1. Definiční obor této funkce je celá reálná osa, funkce je tam spojitá. Protože je to polynom se sudými i lichými mocninami, máme podezření, že není symetrická. Zkusíme jeden symetrický pár: Například f (1) = −9, zatímco f (−1) = 13, což vylučuje možnost, že by f bylo sudé nebo liché.

Než se dostaneme k průsečíkům s osami, potřebujeme se zbavit absolutní hodnoty.

Průsečík s osou x:

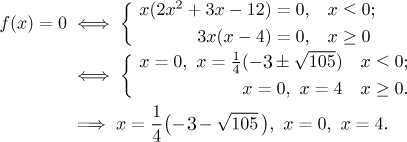
Ty dva ošklivé kořeny u první alternativy jsou přibližně −3.3 a 1.8, takže jsme ten druhý ignorovali, protože příslušná rovnice je relevantní pouze pro nekladná čísla. Všimněte si, že f (0) = 0, takže je to také průsečík s osou y.

Krok 2. Najdeme limity v krajních bodech intervalů definičního oboru.

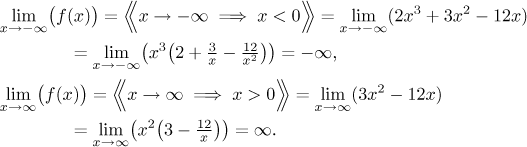
Asymptoty: Protože je daná funkce spojitá na celé reálné ose, nemohou být svislé asymptoty. Protože limity v plus a mínus nekonečnu divergují, nemáme tam vodorovné asymptoty, ale limity existují a proto tam je šance na šikmé asymptoty. Použijeme příslušný algoritmus.

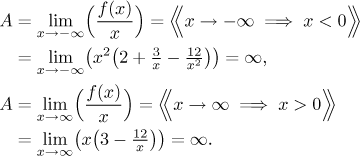
Limita pro A diverguje jak v mínus nekonečnu, tak v nekonečnu, proto tam nejsou šikmé asymptoty.

Krok 3. Najdeme derivaci a použijeme ji k určení monotonie a lokálních extremů. Pro každou alternativu použijeme běžná pravidla, ale připomínáme, že fungují pouze na otevřených množinách.

Kritické body: Je jeden bod definičního oboru, kde derivace možná neexistuje; nejsme si jisti, ale teď to nemusíme řešit, prostě zahrneme bod x = 0 coby podezřelý bod, kde se může měnit monotonie. Kde je derivace nulová?

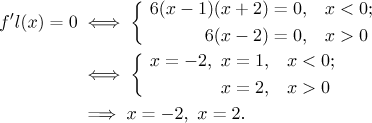
Číslo x = 1 sice vyřešilo první rovnici, ale pro kladná čísla ta rovnice nemá s f ′ nic společného a tudíž to není platný kritický bod. Máme dělící body x = −2, x = 0 a x = 2. Definiční obor se tak rozdělí na čtyři intervaly monotonie, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá. Je třeba být opatrný a použít každý výraz jen v příslušné oblasti.

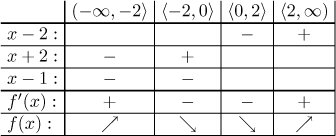
Máme sousedící intervaly stejné monotonie, a protože je f spojitá v bodě jejich dotyku 0, tak víme, že se dají spojit. Závěr je, že f je rostoucí na (−∞,−2⟩ a na ⟨2,∞) a klesající na ⟨−2,2⟩.

Lokální extrémy: Daná funkce má lokální maximum f (−2) = 20 a lokální minimum f (2) = −12. Bod f (0) = 0 není lokální extrém.

Nepotřebovali jsme opravdu vědět, jak je to s derivací v nule, takže jsme výpočet jednostranných derivací přeskočili, ale jejich znalost nám pomůže při kreslení grafu, tak to tady spočítáme, ať máme část o první derivaci kompletní. Najdeme je pomocí limity, viz příslušná věta v sekci Derivace a limita v části Teorie - Věta o střední hodnotě.

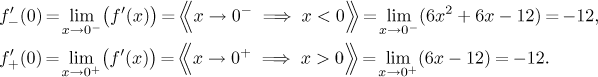
Kupodivu máme v bodě, kde se obě větve spojují, derivaci, f ′(0) = −12. To znamená, že se ty části napojují hladce, bez ostrého ohybu.

Krok 4. Najdeme druhou derivaci a použijeme ji k určení konvexity.

Dělící body: V definičním oboru je jeden bod, kde druhá derivace možná neexistuje; protože to nepotřebujeme opravdu vědět, tak ušetříme čas tím, že to dále nebudeme zkoumat, a prostě bod x = 0 zahrneme mezi dělící body. Druhá derivace je nula pro x = −1/2, což je druhý dělící bod. Definiční obor se tak rozdělí na tři intervaly konvexity, určíme ji pomocí tabulky; krajní body uzavřeme tam, kde je funkce spojitá.

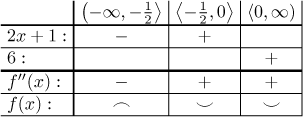
Závěr je, že f je konkávní na (−∞,−1/2⟩; je konvexní na ⟨−1/2,0⟩ a na ⟨0,∞).

Inflexní body: Jeden máme určitě, f (−1/2) = 6+1/2. Není zcela jasné, co se děje v nule. Pomocí limity a jednostranných druhých derivací se ale dá ukázat, že v 0 dokonce máme druhou derivaci, f ′′(0)=6. Funkce je tedy ve skutečnosti konvexní na ⟨−1/2,∞).

Krok 5. Teď to dáme všechno dohromady. Nejprve načrtneme do obrázku všechny body a limitní trendy, které jsme našli. To bude kostra, na kterou pak funkci pověsíme. Abychom ušetřili místo, změníme měřítko na ose y.

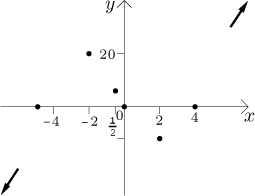
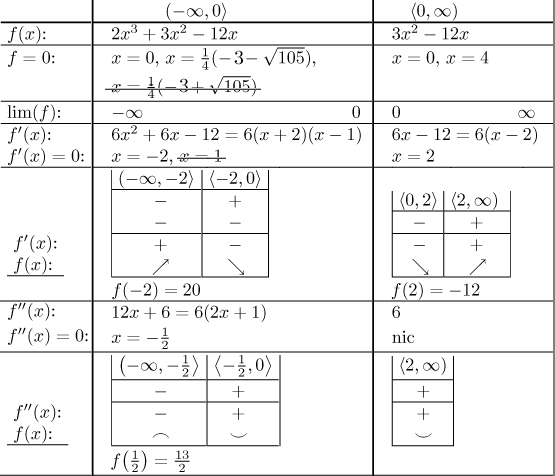
Abychom si tvar grafu lépe představili, zkombinujeme ony dvě tabulky výše.

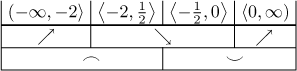
Teď jsme připraveni nakreslit průběh funkce.

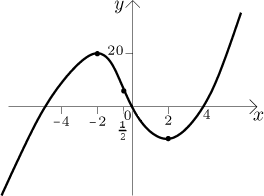
Poznámka: Když pracujeme s funkcemi danými rozpisem, rozdělíme reálnou osu na několik oblastí podle její definice a pak vlastně děláme onen postup několikrát, v každé oblasti zvlášť, a v každé z nich ignorujeme výsledky, které spadají mimo dotyčnou oblast. Předchozí výpočty se dají (stručně) vyjádřit takto.

Další příklad
Zpět na Řešené příklady - Průběh funkce