Příklad: Určete, zda následující řada konverguje.

Řešení: Členy této řady jsou všechny kladné, takže můžeme použít všechny ty báječné testy. Který z nich ale bude fungovat? Protože členy obsahují faktoriály, jasnou volbou je podílové kritérium. Možná ale bude lepší se na členy nejprve podívat blíže, abychom viděli, jak se chovají (připomeňme si definici dvojitého faktoriálu z části Funkce - Teorie - Elementární funkce).

Protože je poslední malý zlomek pro velká k přibližně roven 1, ale je vždy menší než 1, tak není jasné, jak se celý velký zlomek chová, například zda jde k 0. Zkusíme podílové kritérium a uvidíme, co se stane, jako obvykle dáme spolu části se stejným původem.

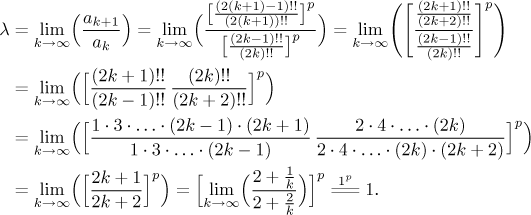
Tohle je pro podílové kritérium neurčitá hodnota, a tak pořád nevíme o dané řadě nic.

Jaké máme jinak možnosti? Faktoriály neumíme integrovat, takže integrální kritérium je mimo hru. Dělat k-tou odmocninu z faktoriálu také není moudré a podle předchozího výsledku bychom stejně dostali ϱ = 1, takže nemá smysl zkoušet odmocninové kritérium. Není tam také vidět nějaké srovnání, takže tradiční testy zde selhávají.

Pokud chceme uspět, musíme hrábnout hlouběji do naší pokladnice, jmenovitě v sekci Další kritéria v části Teorie - Testování konvergence jsme měli testy, které vylepšují podílové kritérium, testy, které (někdy) mohou pomoci, když podílové kritérium vyjde neurčité. Začneme s tím nejjednodušším, limitní verzí Raabeho kritéria.

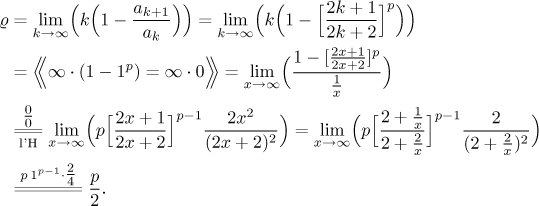
Podle Raabeho kritéria daná řada konverguje, jestliže ϱ > 1, neboli jestliže p > 2, a diverguje, jestliže p < 2. Mimochodem, toto mimo jiné znamená, že členy a_k jdou k nule pro p > 2, tedy i výraz uvnitř (ten podíl faktoriálů) jde k nule. To znamená, že členy řady jdou k nule pro všechna kladná p.

Případ p = 2 zůstává nerozhodnut. Jedna možnost je použít nějakou obecnější verzi Raabeho kritéria. Hlavní myšlenka je podívat se na a_k+1/a_k − 1 a zeptat se, jak hodně je v tom výrazu schováno 1/k.

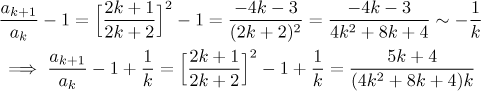
Vidíme, že 1/k je tam jednou, tedy A = 1 v těch obecnějších verzích Raabeho věty, proto nedostaneme konvergenci. Na důkazu divergence ale musíme ještě zapracovat. Jsou dvě možnosti, protože máme dvě obecnější verze Raabeho kritéria. Zkusíme tu, které jsme říkali "nejobecnější".

Pomocí limitního srovnávacího kritéria snadno ukážeme, že řada se členy v_k konverguje, porovnáme ji s p-řadou s p = 2.

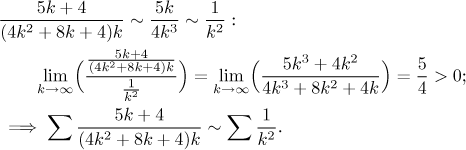
Takže jsme uspěli s přípravou "nejobecnější verze" Raabeho kritéria, máme A = 1, a proto daná řada diverguje pro p = 2.

Závěr: Daná řada konverguje, přesně když p > 2.

Poznámka: Zatímco první krok byl docela přímočarý, rozhodování o případě p = 2 dalo docela práci. Je nějaká alternativa? Kummerovo kritérium je považováno za velmi mocné, ale je vysoce netriviální uhodnout ta pravá p_k, to jde daleko za rámec Math Tutoru. Nevidíme také žádné výhody v kondenzaci. V oné sekci je ještě jeden test, který vypadá slibně, protože Gaussovo kritérium je do značné míry algoritmické. Zkusíme to, uvidíte, že vlastně jenom opakujeme předchozí práci v jiném značení.

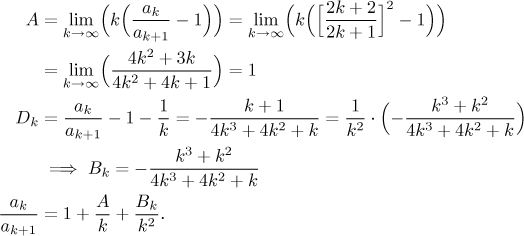
Úspěšně jsme si připravili situaci tak, jak to vyžaduje Gaussovo kritérium, všimněte si, že B_k tvoří omezenou posloupnost a r = 2 > 1. Gaussovo kritérium tedy platí a dostaneme závěr, že daná řada diverguje.

Další příklad
Zpět na Řešené příklady - Testování konvergence