Příklad: Určete, zda následující řada konverguje absolutně.

Řešení: Abychom určili, zda daná řada konverguje absolutně, budeme testovat, zda konverguje následující řada:

Toto je řada s nezápornými členy a máme k dispozici všechny ty báječné testy. Který z nich zabere? Protože se řada skládá z mocnin (a odmocnin), nejlepší pro ni bude nějaké srovnání. Odhadneme, že pro velká k je část "+1" zanedbatelná a lze ji ignorovat. Jedna možnost je prosté srovnání nerovností.

Řada napravo je divergentní (podle p-testu, p = 1/2 < 1), ale naše řada je menší a to je přesně případ, kdy není možné udělat závěr. Zkusíme tedy limitní srovnávací kritérium. Nejprve potvrdíme, že se opravdu dá část "+1" ignorovat, pak můžeme něco tvrdit o podobnosti.

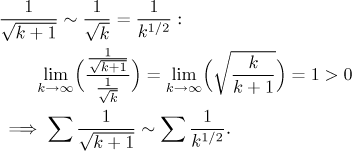
Teď už můžeme použít divergenci testovací řady k závěru, že je naše řada divergentní.

Závěr: Daná řada není absolutně konvergentní.

Je nějaký jiný způsob, jak dokázat divergenci? Víme, že odmocninové kritérium a podílové kritérium nefungují pro řady s polynomy (a odmocninami). A opravdu, dostaneme neurčitou hodnotu 1.

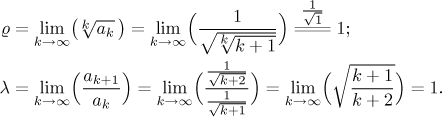
Poslední možnost: Členy řady jsou dány funkcí f (x) = (x + 1)^−1/2, která je kladná a klesající, takže můžeme použít integrální kritérium a přejít od naší řady k příslušnému nevlastnímu integrálu.

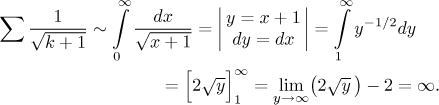
Takže integrální kritérium potvrzuje divergenci řady s absolutní hodnotou.

Poznámka: Řada samotná je konvergentní. Je to alternující řada a členy b_k = (k + 1)^−1/2 jsou kladné, klesající a jdou k nule, takže Leibnizovo kritérium potvrzuje konvergenci této řady.

Další příklad
Zpět na Řešené příklady - Testování konvergence