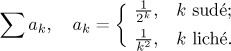
Příklad: Vyšetřete konvergenci následující řady. (Konverguje? Pokud ano, jak?)

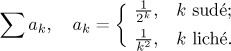
Řešení: Všimněte si, že všechny členy řady jsou kladné, takže je u ní konvergence a absolutní konvergence totéž. Zbývá tedy otestovat konvergenci a pro řadu s kladnými členy máme všechny ty báječné testy.

Protože se členy řady skládají z mocnin, přirozeným kandidátem by mělo být podílové kritérium. Kvůli podvojné podstatě členů se podíváme, co odpovídající podíly dělají pro sudá a lichá k. Pomocí l'Hôpitalova pravidla dostaneme

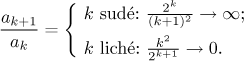
Vidíme, že se posloupnost {a_k+1/a_k} skládá ze dvou podposloupností, jedna jde do nekonečna a druhá k nule. Celá posloupnost tedy nemůže konvergovat a nemáme žádné λ. Mohla by pomoci obecnější verze podílového kritéria (viz Odmocninové a podílové kritérium v části Teorie - Testování konvergence)? Vzhledem k těm dvěma podposloupnostem výše (sudé a liché členy) hned dostaneme, že limes superior je nekonečno, takže toto nepomůže. Co takhle obecná verze s nerovnostmi? Protože jedna podposloupnost jde k číslu menšímu než 1 a druhá k číslu většímu než 1, nedokážeme celou posloupnost přinutit zůstat nad 1, popřípadě zůstat ostře pod 1. Víc verzí není, podílové kritérium zcela proapdlo.

Což takhle odmocninové kritérium? Nejprve se zase podíváme, co dělají sudé a liché členy.

Zase tedy nemáme limitu. Tentokráte je limes superior konečné, ale je to 1 a tudíž to nepomůže. Což takhle obecná verze s nerovnostmi? Všimněte si, že všechny členy (a_k)^1/k jsou menší než jedna, takže obecné odmocninové kritérium nemůže dát divergenci, ale také se (alespoň některé z nich) blíží libovolně blízko k 1, takže také nejsme schopni použít část o konvergenci. Proto ani odmocninové kritérium nepomůže.

Jaký další test by mohl pomoci? Protože členy nejsou dány jedním vzorcem, integrální kritérium je mimo hru. Naše jediná naděje teď spočívá v nějakém srovnání. Výsledky výše naznačují, že limitní srovnání není možné, protože sudé a liché členy se chovají zcela rozdílnými způsoby; škála mocnin ukazuje, že sudé členy jdou k nule neporovnatelně rychleji než liché členy.

Jedinou nadějí je tedy srovnání. Poslední věta předchozího odstavce už naznačuje jednu možnost. Je relativně snadné ukázat, že pro k alespoň 5 je 2^k větší než k² (nebo se odvoláme na již zmíněnou škálu mocnin a usoudíme, že taková nerovnost musí platit pro velká k), proto dostaneme srovnání

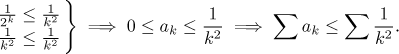
Protože řada napravo konverguje (viz p-test nebo Příklad tamtéž, tato řada je velmi známá), vyplývá z toho, že také daná řada konverguje, proto také konverguje absolutně.

Alternativa: Je tu ještě jiný zajímavý trik, který by se dal zkusit. Daná řada má členy dvou typů, proto je můžeme rozdělit do dvou samostatných řad. Vyjádříme ji tedy jako součet  ∑ b_k  a  ∑ c_k,  kde

Co se dá říct o konvergenci těchto dvou řad? Na první pohled jsme si moc nepomohli, zase jsou obě takové dvojité, jenže - a to je právě ta finta - nuly se dají z řady bez problémů vypustit. Řady je tedy možno přepsat pomocí obvyklých výrazů pro sudá a lichá čísla následovně.

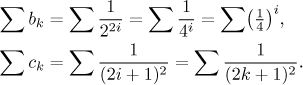
Vidíme, že první řada je geometrická řada s |q| < 1, proto konverguje. Druhou řadu jsme si přepsali na tradiční index k, nebylo to nutné, ale je dobré si trochu pomoci, jsme na takový index zvyklí. Vidíme rovnou, že i tato druhá řada je konvergentní, dokáže se to například tímto srovnáním s řadou, již jsme už viděli.

Součet dvou konvergentních řad zase konverguje, čímž jsme potvrdili konvergenci dané řady.

Další příklad
Zpět na Řešené příklady - Testování konvergence