Příklad: Vyšetřete konvergenci následující řady. (Konverguje? Pokud ano, jak?)

Řešení: Máme se podívat na konvergenci dané řady a také její absolutní konvergenci. Začneme tím prvním. Co víme o členech řady? Čísla cos(kπ/2) nabývají hodnot 1, 0, −1, 0, 1, 0,..., což znamená, že daná řada mění znaménka, ale nejsou alternující. Nemůžeme tedy přímo použít Lebnizovo kritérium. Co ještě zbývá? Jsou dvě možnosti. Jedna je použít Dirichletovo kritérium. Čísla a_k = cos(kπ/2) a b_k = 1/(k² + 1) totiž opravdu splňují jeho předpoklady, mimo jiné částečné součty řady

1 + 0 − 1 + 0 + 1 + 0 − 1 + ...

jsou jen 0 a 1. Toto dokazuje, že daná řada je konvergentní.

Mohli bychom také použít Fakt formulovaný tamtéž, který se dívá na Dirichletovo kritérum jako na zobecnění Leibnizova kritéria a platí pro řady s pravidelným vzorem znamének, jejichž součet přes jednu periodu je nula - přesně naše situace.

Dá se konvergence nějak odvodit bez použití pokročilejších testů, jen s těmi základními, které zná každý student kalkulu? Ano, je. Když se na danou řadu podíváme pořádně, tak zjistíme, že je to vlastně alternující řada, jen si musíme všimnout, že všechny členy s k lichým jsou nulové, takže je lze vypustit a řadu příslušným způsobem přeindexovat.

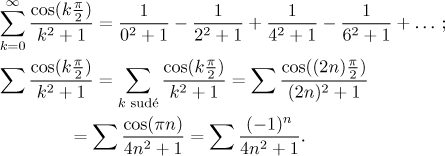
Teď vidíme, že řada je vlastně opravdu alternující, takže použijeme Leibnizovo kritérium s b_k = 1/(4k² + 1) a dostaneme závěr, že řada je konvergentní.

Teď se podíváme na absolutní konvergenci. Chceme zkoumat konvergenci řady

Její členy jsou všechny nezáporné, ale kosinus nevypadá příliš přítulně. Absolutní hodnota vylučuje integrování, takže od integrálního kritéria nic nečekejme. Protože posloupnost |cos(kπ/2)| nemá limitu, dají se čekat potíže se všemi testy, které používají limitu, takže se také necítíme na to zkoušet odmocninové kritérium či podílové kritérium. Nakonec se tedy dostáváme k srovnávacím kritériím, což je zde vlastně přirozený přístup. Pro řady s polynomy je totiž srovnání doporučenou metodou, navíc tu máme přirozenou horní mez pro část, která se nám nelíbí. Odhadujeme:

Máme pěkné srovnání a o řadě napravo víme, že konverguje, například podle p-testu. Máme tedy závěr, že řada nalevo je také konvergentní.

Závěr: Daná řada je absolutně konvergentní.

Poznámka: Protože absolutní konvergence implikuje konvergenci, mohli jsme si ušetřit práci, kdybychom začali rovnou absolutní konvergencí.

Poznamenejme, že protože čitatel s kosinem nemá limitu, tak se nemá smysl ptát, jak to vypadá pro velká k. Pro tuto řadu tedy nelze použít limitní srovnávací kritérium. Máme zde příklad řady, pro kterou srovnání funguje, ale limitní srovnání ne.

Poznámka: Všimněte si, že když použijeme naše alternativní vyjádření pro danou řadu, pak se naše situace se zkoumáním absolutní konvergence podstatně zjednoduší.

Teď můžeme použít všechny testy, ale některé nepomůžou. Víme, že pro řady s racionálními lomenými funkcemi je nejlepší přístup přes srovnání, většinou jeho limitní verze. V tomto případě jsou možná obě srovnání a vedou na správnou odpověď.

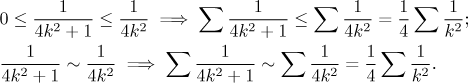
Protože je funkce f (x) = 1/(4x² + 1) kladná, klesající a relativně snadno se integruje, také integrální kritérium je rozumná možnost.

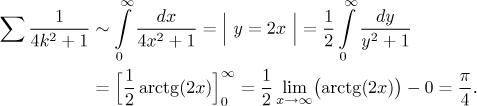
Na druhou stranu, víme že řady s racionálními lomenými funkcemi se nedají řešit přes odmocninové kritérium nebo podílové kritérium, protože dostaneme neurčitý výsledek. A opravdu,

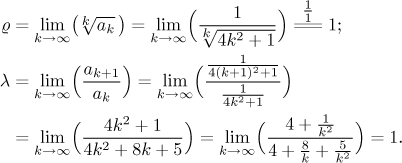
Další příklad
Zpět na Řešené příklady - Testování konvergence