Posloupnosti funkcí

Začneme definicí posloupnosti funkcí a většinu této sekce budeme věnovat zkoumání konvergence, obzvláště problému zachování vlastností. Nakonec nám nezbyde než uvést na scénu stejnoměrnou konvergenci. Na konci se stručně podíváme na monotonii.

Definice.
Posloupností funkcí myslíme libovolnou spočetnou uspořádanou množinu

{ f_k}_{k ≥ n0} = { f_n0,  f_n0+1,  f_n0+2,...},

kde f_k jsou funkce a počáteční index n₀ je nějaké celé číslo.

Podle toho, jaké funkce uvažujeme, dostaneme různé teorie. Zde budeme uvažovat pouze reálné funkce, tedy funkce definované na podmnožinách reálných čísel a s reálnými hodnotami. Další populární volba jsou komplexní funkce a vlastně většina výsledků zde se dá přenést s malými (a většinou zjevnými) modifikacemi na komplexní případ, ale to je za obzorem Math Tutoru.

Naším hlavním zájmem je teď rozvinout pojem konvergence pro posloupnosti funkcí, v kterémžto případě nám vlastně nezáleží na začátku dané posloupnosti. Pak si - jako obvykle - zjednodušíme život tím, že budeme prostě psát { f_k}.

Pokud chceme studovat posloupnosti funkcí, tak je dobrým začátkem si představit jejich grafy. Máme jeden obrázek s osami a do něj vkreslíme nekonečně mnoho grafů. Pokud se má stát něco rozumného, tak potřebujeme alespoň malý kousek reálné osy, kde všechny tyto funkce opravdu existují. Jinými slovy, celá naše práce v této a následujících sekcích je založena na nevyřčeném předpokladu, že definiční obory všech f_k mají neprázdný průnik. Pak pracujeme na tom průniku a v zásadě ignorujeme vše, co se děje mimo tuto společnou množinu. Správný začátek tedy je představit si nějakou pěknou množinu na reálné ose (třeba interval) a na ní nekonečně mnoho funkcí (grafů).

Než se dostaneme k hlavní definici, zkusíme vymyslet, co má vlastně smysl. Nejpřirozenější přístup k posloupnostem libovolného druhu je vrátit se k tomu, co už známe - posloupnostem (reálných) čísel. Je-li dána posloupnost funkcí { f_k}, můžeme zvolit jisté číslo x z průniku definičních oborů a dosadit jej do všech těchto funkcí. Každé f_k(x) je pak číslo, dostaneme tedy posloupnost reálných čísel { f_k(x)}. S těmito už umíme pracovat; například už víme, jak zjistit, zda je taková posloupnost konvergentní nebo ne. Pokud je, tak dostaneme nějakou limitu A - reálné číslo.

Když toto zkusíme pro všechna čísla x z toho průniku definičních oborů, tak uvidíme, že se tento průnik rozpadne na dvě části. Pro některá x výsledná reálná posloupnost nekonverguje. Pro jiná ano, tyto tvoří obor konvergence pro danou posloupnost funkcí. Pro každé x z této oblasti dostaneme příslušnou limitu A posloupnosti { f_k(x)}, měli bychom vlastně správně psát něco jako A_x, protože hodnota této limity evidentně záleží na volbě x. Jaká je teď situace? Dostali jsme rozumnou posloupnost funkcí (jejichž definiční obory mají neprázdný průnik) a určili jsme obor konvergence. Může být prázdný, ale pokud není, tak máme určitou podmnožinu reálných čísel a ke každému x z této množiny máme přiřazenu určitou hodnotu, jmenovitě limitu A_x. Jinými slovy, máme novou funkci, říkejme jí f. Jestliže chceme vědět, kolik je f (x), tak vezmeme toto x a najdeme limitu { f_k(x)}. Této funkci f budeme přirozeně říkat limita posloupnosti { f_k}. Jsme připraveni na formální definici a nějaké pěkné příklady.

Definice.
Uvažujme posloupnost funkcí { f_k}.
Definujeme její obor konvergence jako množinu všech x, pro která jsou všechny f_k definovány a posloupnost { f_k(x)} konverguje.
Na tomto oboru konvergence definujeme funkci f zvanou limita posloupnosti { f_k} vzorcem

Protože se teď soustředíme na funkce a ne čísla (jinými slovy, dáváme teď přednost mluvit abstraktně, o funkcích jako o objektech), tak bychom dali přednost značení, které se neodvolává na body. Fak, že je funkce f limitou posloupnosti funkcí { f_k}, se značí takto:

My ale víme, že při práci s funkcemi je zásadní vědět, kde žijí a kde věci fungují, což z toho značení pomocí "lim" nepoznáme. Obor konvergence nemá žádné všeobecně přijímané značení, už proto, že někdy stejně raději pracujeme na ještě menší množině. Proto zavedeme následující obecnější úmluvu. Jestliže je M nějaká podmnožina oboru konvergence (například přímo obor samotný), pak řekneme, že posloupnost { f_k} konverguje k f na M. Často raději mluvíme o funkcích samotných, spíš než o posloupnosti, kterou tvoří, takže lidé také říkají, že funkce f_k konvergují k f na M. Obě tvrzení se dají zapsat jako

f_k→f na M.

Brzy uvidíme, že jsou další způsoby, jak se dívat na konvergenci funkcí. Je všeobecně akceptováno, že když se mluví o konvergenci bez nějaké další specifikace, tak se tím rozumí ta, kterou jsme právě definovali, už proto, že je v jistém smyslu základní a ty další typy konvergence obvykle fungují tak, že jen přidají další požadavky k tomuto pojmu, který už máme. Někdy ale chceme zdůraznit, že opravdu myslíme tuto konvergenci, že se opravdu díváme na chování v jednotlivých bodech. Pak říkáme, že f_k konvergují bodově k f na M.

Poznámka: Když jsme pracovali s posloupnostmi reálných čísel, zajímal nás také jeden speciální případ divergence, když byla limita nekonečná. Zde nás to nezajímá, protože ten pravý typ objektu, který chceme obdržet jako limitu, je zase funkce, a té nemůžeme přiřadit hodnotu nekonečno.

Příklad: Uvažujme posloupnost dánu vzorcem f_k(x) = x^k pro k = 1,2,3,...

Všechny tyto funkce jsou definovány na celé reálné ose, takže množina reálných čísel je naším východiskem při zkoumání konvergence posloupnosti funkcí {x^k}. Když pevně zvolíme libovolné reálné číslo, stane se konstantou, tudíž se z posloupnosti {x^k} stane geometrická posloupnost. Pokud totiž například vezmeme x = 2, pak dostaneme posloupnost {2^k}. Jestliže vezmeme x = −1/2, dostaneme posloupnost {(−1/2)^k} atd. Víme velmi dobře, jak se geometrické posloupnosti chovají, jejich konvergence závisí na bázi, na zvoleném čísle x. Proto také víme, že jestliže |x| < 1, pak {x^k} konverguje k 0, a jestliže x = 1, pak {x^k} = {1^k} = {1} konverguje k 1. Víme také, že všechny jiné volby x dávají divergentní geometrickou posloupnost. Máme tedy následující závěr:

Obor konvergence dané posloupnost je interval (−1,1⟩ a na tomto intervalu máme

Pokud výslednou funkci nazveme f, pak také můžeme napsat, že x^k→f na (−1,1⟩. Následující obrázek naznačuje, co se děje, nakreslili jsme prvních pět funkcí dané posloupnosti. Nalevo se díváme na větší část reálné osy, ale funkce utečou příliš rychle na to, abychom dobře viděli ten zajímavý úsek okolo počátku. Proto se na něj soustředíme v obrázku napravo a ukážeme více mocnin (přesně řečeno až po x¹⁰).

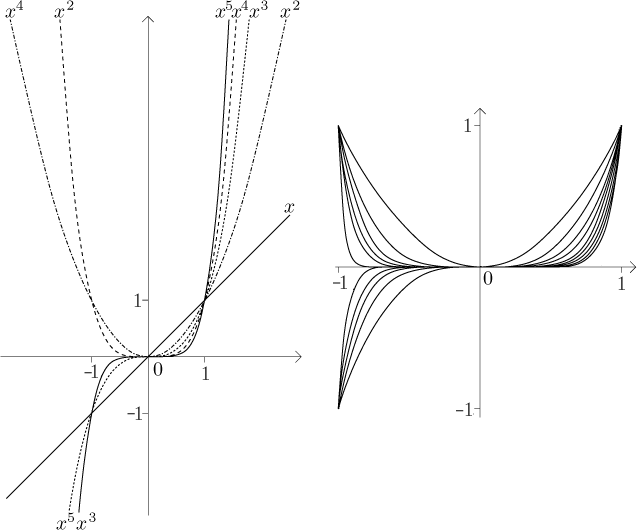
Vidíme, že se grafy x^k na (−1,1) coby křivky blíží k ose x neboli k funkci 0 (pokud chcete vidět animaci, klikněte si sem). Ještě se k tomuto příkladu později vrátíme.

Příklad: Uvažujme posloupnost danou vzorcem f_k(x) = arctg(k⋅x) pro k = 1,2,3,...

Všechny tyto funkce jsou definovány na celé reálné ose, takže množina reálných čísel bude našim východiskem při zkoumání posloupnosti funkcí {arctg(kx)}. Když pevně zvolíme libovolné reálné číslo, tak pro kladná x jde posloupnost {kx} do nekonečna pro k jdoucí do nekonečna a arkus tangens je tam roven π/2. Jestliže je x záporné, tak jde {kx} do mínus nekonečna a arkus tangens je tam roven -π/2. Jestliže x = 0, pak po dosazení do posloupnosti {arctg(kx)} se z ní stane posloupnost {0} konvergující k 0. Máme tedy

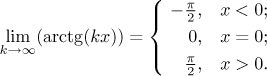
Obrázek zase ukáže, co se děje.

S rostoucíím k se křivky (grafy) stále více přimykají ke konstantním funkcím -π/2 a π/2.

Protože je pojem konvergence pro funkce odvozen od pojmu konvergence pro reálná čísla, mnohé z pěkných vlastností se zachovají. Za prvé, konvergence funkcí se chová velice pěkně vzhledem k obvyklým algebraickým operacím.

Věta.
Předpokládejme, že posloupnost funkcí { f_k} konverguje k funkci f na množině M a že posloupnost funkcí {g_k} konverguje k g na téže množině M. Pak platí následující:
(i)  Pro libovolné reálné číslo a konverguje posloupnost {a⋅ f_k} k a⋅ f na M.
(ii)  Posloupnost { f_k + g_k} konverguje k f + g na M.
(iii)  Posloupnost { f_k − g_k} konverguje k f − g na M.
(iv)  Posloupnost { f_k⋅g_k} konverguje k f⋅g na M.
(v)  Posloupnost { f_k/g_k} konverguje k f/g na množině všech x z M, pro které jsou všechny g_k(x) různé od 0.
(vi)  Posloupnost { f_k^g_k} konverguje k f ^g na množině všech x z M, pro které jsou všechny f_k(x) kladné.

Krátce řečeno, operace fungují kdykoliv a kdekoliv má výsledek smysl (co se týče té poslední podmínky, připomeňte si, jak jsme pracovali s obecnými mocninami). Poznamenejme, že první dvě tvrzení se dají spojit do tvrzení, že pojem limity splňuje linearitu.

Skládání je zákeřné. Limita si se skládáním funkcí rozumí jen za velice specifických podmínek, viz například příslušná věta v sekci Základní vlastnosti v části Posloupnosti - Teorie - Limita. Nenabídneme proto žádné obecné tvrzení, které by říkalo něco jako že by f_k(g_k) mělo konvergovat k f (g), toto selhává dokonce i pro spojité funkce. Pokud něco takového chceme, pak máme dvě možnosti. Buď vylepšíme konvergenci, což je něco, co přijde později. Druhá možnost je spokojit se s méně obecnou situací a pracovat jen s jednou posloupností.

Věta.
(i)  Předpokládejme, že posloupnost funkcí { f_k} konverguje k funkci f na množině M a že funkce g zobrazuje N do M. Pak posloupnost { f_k(g)} konverguje k f (g) na N.
(ii)  Předpokládejme, že posloupnost funkcí {g_k} konverguje k funkci g na množině N, funkce f je spojitá na M a všechny g_k zobrazují N do M. Pak posloupnost { f (g_k)} konverguje k f (g) na N.

Některé vlastnosti funkcí jsou konvergencí zachovány.

Věta.
Předpokládejme, že posloupnost funkcí { f_k} konverguje k funkci f na množině M.
(i)  Jestliže jsou všechny f_k liché, pak je také f lichá.
(ii)  Jestliže jsou všechny f_k sudé, pak je také f sudá.
(iii)  Jestliže jsou všechny f_k T-periodické, pak je také f T-periodická.
(iv)  Jestliže jsou všechny f_k neklesající funkce, pak je také f neklesající funkce.
(v)  Jestliže jsou všechny f_k nerostoucí funkce, pak je také f nerostoucí funkce.
(vi)  Jestliže jsou všechny f_k konstantní funkce, pak je také f konstantní funkce.

Poslední tvrzení si říká o vysvětlující poznámku. Mluvíme tam o posloupnosti konstant. Každá funkce jako jednotlivec je konstatní, ale každá může být jiná. Na druhou stranu konstantní posloupnost funkcí je posloupnost, kde jsou všechny funkce stejné, ale ne nutně konstantní, například pokud f_k(x) = x² pro všechna k, tak dostaneme konstantní posloupnost, a tato evidentně konverguje k x². Obecně konstantní posloupnost konverguje k onomu konstantnímu prvku - přesně jako u reálných posloupností.

Viděli jsme (viz Funkce - Teorie - Limita a srovnání), že přechodem k limitě se může nerovnost změnit v rovnost, ale nikdy ne v opačnou nerovnost. Tím se vysvětluje, proč v (iv) a (v) výše monotonie přežívá, ale ryzí monotonie ne, viz níže.

Viděli jsme některé vlastnosti, které se zachovávají, ale bohužel u těch opravdu zajímavých se na jejich přežití spoléhat nemůžeme. Zejména máme:
(1) i když jsou všechny  f_k prosté,  f nemusí být prostá;
(2) i když jsou všechny  f_k rostoucí,  f nemusí být rostoucí;
(3) i když jsou všechny  f_k klesající,  f nemusí být klesající;
(4) i když jsou všechny  f_k omezené,  f nemusí být omezená;
(5) i když jsou všechny  f_k spojité,  f nemusí být spojitá;
(6) i když jsou všechny  f_k diferencovatelné,  f nemusí být diferencovatelná;
(7) i když jsou všechny  f_k integrovatelné,  f nemusí být integrovatelná.

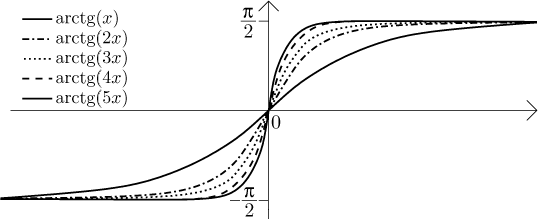
Například ty arkus tangensy v posledním příkladě jsou rostoucí, prosté, spojité a mají všude derivace všech řádů, ale jejich limita není ani spojitá v 0, nemluvě o diferencovatelnosti, a také porušuje striktní monotonii a prostotu skoro nejvíc, co to jde. Coby spojité funkce jsou ty arkus tangensy integrovatelné a mají primitivní funkce na reálné ose, ale jejich limita f nemá primitivní funkci okolo počátku kvůli tomu skoku.

Abychom viděli, že omezenost nemusí přežít, uvažujme tento příklad: Jestliže definujeme f_k(x) = min(e^x,k), dostaneme posloupnost omezených funkcí. Každá funkce je prostě jen exponenciála uříznutá na úrovni k a nahrazená tam konstantou. Jsou tedy všechny opravdu omezené, ale tato posloupnost evidentně konverguje na reálné ose k e^x a to není omezené.

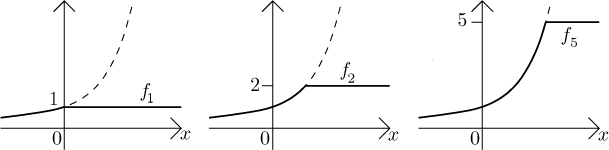
Je nějaký způsob, jak tuto nemilou situaci zachánit? Nejsou rozumné podmínky, které by zachránily (1)--(3). Ostatní čtyři se dají zachránit, pokud bychom požadovali, aby byla konvergence "lepší" (viz následující část níže). Vlastně se dá také zachránit (4) tím, že bychom po dané posloupnosti požadovali "stejnoměrnou omezenost", a (5) požadavkem, aby všechny funkce byly "stejnoměrně spojité", ale to už je pokročilý materiál a nebudeme tady do toho šťourat (také se používá méně než ona "lepší konvergence", kterou zde ukážeme).

Než se k té nové konvergenci dostaneme, podíváme se blíže na poslední tři problémy (5)--(7). Ukážeme, že ve skutečnosti reprezentují myšlenku "záměny operací". U spojitosti to funguje následovně. Nejpraktičtější způsob určení spojitosti je přes limitu (viz Spojitost v části Funkce - Teorie - Reálné funkce). Uvažujme posloupnost { f_k} spojitých funkcí konvergující k nějakému f. Nechť a je nějaký bod ve vnitřku oboru konvergence. Funkce f je tam spojitá, přesně když je její hodnota v a stejná jako její limita v a. Podíváme se teď na tuto podmínku blíže, v posledním kroku použijeme předpoklad, že f_k jsou spojité.

Je-li dána posloupnost funkcí { f_k}, jsou dvě věci, kterými můžeme hýbat - index k a proměnná x. V dokonalém světě by v případě, kdy chceme aplikovat limitu na obě tyto kvantity, nezáleželo na pořadí. Teď ale vidíme, že zaměnitelnost pořadí limit je ekvivalentní zachování spojitosti, a o tom víme, že to neplatí. Konec konců, můžeme ten příklad s arkus tangensy výše použít jako pěknou ukázku, že na pořadí aplikace limit záleží.

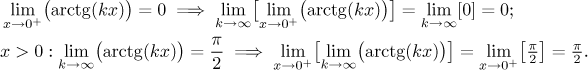
Tento problém se objevuje v mnoha situacích, kdy aplikujeme limitu na více objektů, například u funkcí více proměnných, takže otázka prohoditelnosti limit je dosti důležitá. Rozhodně stojí za to se zeptat, za jakých okolností se to může udělat.

Problém s derivací, tak jak je nahoře položen, není přesně tohoto typu, ale my ve skutečnosti většinou chceme víc, než co je tam napsáno. Pokud máme diferencovatelné funkce f_k, které konvergují k nějaké f na množině M, tak bychom rádi, aby f byla diferencovatelná a aby se její derivace f ′ dala získat jako limita derivací f_k′. Jinými slovy, chceme mít svobodu volby, zda nejprve děláme limitu a pak derivujeme či naopak.

Tato zaměnitelnost limity a derivace je také docela problém. Příklad s arkus tangensy výše ukazuje, že je možné diferencovatelnost zcela ztratit, ale může se také stát, že f derivaci má, ale nedokážeme se k ní dostat pomocí  f_k, viz například tento příklad v části Řešené příklady - Řady funkcí.

To nás přivádí k problému s integrací. Tak je to dokonce ještě komplikovanější. Jestliže integrovatelné funkce f_k konvergují k f na nějakém M, pak nemůžeme doufat, že by jejich primitivní funkce F_k šly k F už z toho jednoduchého a zásadního důvodu, že každá funkce má nekonečně mnoho primitivních funkcí; můžeme si pro každou funkci jednu primitivní zvolit, ale pak nejspíše nedají dohromady konvergentní posloupnost, protože jejich různé posuny dost zatočí s konvergencí.

Jsou dva rozumné způsoby, jak z toho vybruslit. Jedna možnost je použít určitý integrál, takže se dá například žádat, aby pro libovolný interval mezi a a b, který leží zcela v M, platilo

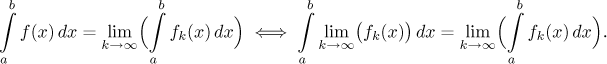
Zase tedy vlastně chceme měnit pořadí dvou operací, limity a (určitého) integrování. Ta druhá možnost je použít určitý integrál od nějakého pevně zvoleného a do proměnné x, čímž obdržíme jednu specifickou volbu primitivní funkce, což má smysl, pokud je obor konvergence interval.

I zde se může stát, že f integrovatelné je, ale tento integrál nemá nic společného s integrály f_k. Uvažujme následující funkce.

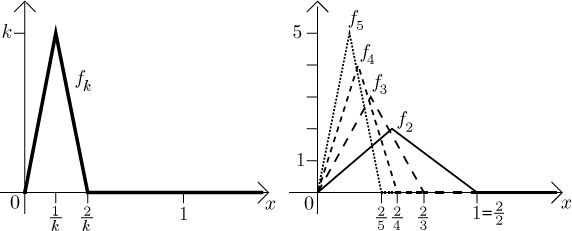
Všimněte si, že když procházíme posloupností, tak trojúhelníky kloužou směrem k 0. Pokud si tedy zvolíme nějaké kladné x, tak jej tyto kopce dřív či později minou a f_k(x) začnou být 0, takže f_k konvergují k 0 pro x > 0. V x = 0 prostě všechny jsou nula. Toto dokazuje, že { f_k(x)} konverguje k f = 0 na ⟨0,∞). Teď se soustřeďme na interval ⟨0,1⟩. Všechny funkce zde vystupující jsou spojité a tudíž i integrovatelné, ale integrál přes ⟨0,1⟩ funkce f je 0, zatímco všechny f_k tam mají integrál 1. Proto nelze integrál f získat pomocí integrálů f_k.

Ukázali jsme, že poslední tři problémy (5)--(7) jsou svázány s otázkou zaměnitelnosti pořadí limity, derivace a integrálu. Teď se podíváme na nějaké kladné výsledky.

Než ukážeme její definici, ukážeme, proč je to ta pravá. Když jsme ztratili spojitost a víc v prvních dvou příkladech, opravdovým důvodem byly rozdílné rychlosti konvergence. Víme například, že pro |x| < 1 jde posloupnost x^k k 0, ale pro různá x tam jde rozdílnou rychlostí; čím je x blíže k 1 (nebo −1), tím déle to trvá, než se x^k dostane k 0. Obrázky výše to konec konců ukazují dost jasně. Stejná věc platí pro druhý příklad, čím blíže k nule se podíváme, tím déle to arkus tangensům trvá, než se dostanou ke své limitě.

Je ještě jeden způsob, jak to vyjádřit. Jedna z možných interpretací limity je přes aproximaci. Jestliže čísla a_k konvergují k A, pak pro každou toleranci ε existuje nějaké a_K, které aproximuje A až na to ε. Funguje to pro funkce? První dva příklady ukazují, že konvergence jak jsme ji definovali tak nefunguje. Například funkce x^k konvergují k funkci 0 na (0,1), ale když zvolíme řekněme ε = 1/2, tak není index K takový, aby x^K bylo 0 až na chybu 1/2, každá mocnina vyskočí příliš vysoko poblíž 1. Bodová konvergence je tedy pěkná, ale ne zcela to, co bychom očekávali. Potřebujeme nějakou lepší.

Základní myšlenka stejnoměrné konvergence je opravit výše popsanou vadu. Umožní nám aproximovat limitní funkci f libovolně dobře určitou f_k, ekvivalentně vyjádřeno, nutí to f_k konvergovat k f všude stejnou rychlostí. Myšlenka je jednoduchá: Místo toho, abychom hráli limitní hru zvlášť pro každý bod, budeme ji hrát zároveň všude na celé množině konvergence.

Definice.
Uvažujme posloupnost funkcí { f_k}. Nechť je M množina, na které jsou všechny f_k definovány.
Řekneme, že posloupnost { f_k} konverguje k f stejnoměrně na M, jestliže pro každé ε > 0 existuje celé číslo N takové, že pro každé k ≥ N a pro každé x z Mplatí

| f_k(x) − f (x)| < ε.

Značíme to f_k ⇉ f na M.

Začneme jednoduchým pozorováním:

Fakt.
Uvažujme posloupnost funkcí { f_k} a funkci f.
Jestliže f_k ⇉ f na M, pak f_k→f na M.

Toto ukazuje, že stejnoměrná konvergence je opravdu silnější než bodová konvergence, a níže ukážeme, že je dost silná na to, co od ní chceme. Ukazuje to také, že dokazovat stejnoměrnou konvergenci má smysl jen na podmnožinách oboru konvergence { f_k}. No a konečně to také ukazuje způsob, jak stejnoměrnou konvergenci určit. Dělat to podle definice není praktické, první z mnoha problémů je, kde vezmeme to záhadné f. Tento Fakt ukazuje, že prostě vezmeme f z bodové konvergence, což je něco, co obvykle umíme dobře. K obejití nepříjemné epsilon-delta hry nám pomůže další pozorování.

Fakt.
Uvažujme posloupnost funkcí { f_k} a funkci f. Nechť je M nějaká podmnožina oboru konvergence { f_k}.
Pak f_k ⇉ f na M tehdy a jen tehdy, když čísla  sup_M| f_k − f |  konvergují k 0 pro k jdoucí do nekonečna.

Tohle není nic hlubokého, jen mírně odličný způsob napsání definice; supremum nám říká, jak dobrá je aproximace f pomocí nějaké konkrétní f_k globálně na množině M, a my chceme, aby se ty aproximace zlepšily na tak dobré, jak jen budeme chtít. Protože se supremum dá často určit (nebo alespoň odhadnout), je toto velmi parktické. Tu f dostaneme z bodové konvergence a nalezení suprema funkce je také standardní problém.

Příklad: Uvažujme posloupnost danou předpisem  f_k(x) = x^k. Ukázali jsme, že konverguje ke konstantní funkci 0 na M = (−1,1), ale naše předchozí pozorování silně naznačují, že tato konvergence není stejnoměrná. Teď to dokážeme: Pro každé k dostaneme

sup_M| f_k(x) − f (x)| = sup{|x^k|; −1 < x < 1} = 1.

Vidíme, že kvalita aproximace (neboli rychlost konvergence) se opravdu zhoršuje poblíž 1 a −1, takže stejnoměrnou konvergenci dostaneme odříznutím těchto bodů. Vezměme libovolné kladné číslo a < 1, je dobré si jej představit velice blízko k 1. Uvažujme množinu M = ⟨-a,a⟩. Pro každé x z této množiny máme |x^k| ≤ a^k, proto teď

sup_M| f_k(x) − f (x)| = sup{|x^k|; −a ≤ x ≤ a} = a^k→0.

V posledním kroku (při výpočtu limity) jsme použili fakt, že |a| < 1. Právě jsme dokázali, že x^k konverguje stejnoměrně k 0 na všech intervalech ⟨-a,a⟩ s a < 1. Toto potvrzuje, co jsme předtím odhadli. Problém s konvergencí na intervalu (−1,1) je v 1 a v −1, čím blíže se dostaneme, tím horší konvergence. Když tyto konce odřízneme, dokonce i když odřízneme jen malilinkatý kousek (a může být libovolně blízko k 1), tak se situace dramaticky zlepší. Toto je vlastně dosti typické, rozumná řada má potíže s konvergencí u koncových bodů svého oboru konvergence (konec konců, konvergence tam "končí", a nevypadá moc přirozeně, že by prostě náhle skončila, v typickém případě se postupně zhoršuje, až nakonec selže zcela). Když tyto konce odřízneme, konvergence se stane stejnoměrnou. Toto chování uvidíme v mnoha řešených příkladech na toto téma, viz Řešené příklady - Řady funkcí. Některé posloupnosti jsou dokonce ještě lepší, ty konverují stejnoměrně všude, zase viz Řešené příklady.

Podobně snadno se ukáže, že v příkladě s klouzajícími trojúhelníky výše není konvergence stejnoměrná na ⟨0,∞), díky těm vzrůstajícím trojúhelníkům jde příslušné supremum dokonce do nekonečna, ale jakmile odřízneme počátek tím, že uvažujeme ⟨a,∞) pro nějaké a > 0, dostanem už stejnoměrnou konvergenci.

Stejnoměrná konvergence je znatelně lepší než bodová konvergence. Připomeňme například, že jsme měli potíže se skládáním. Se stejnoměrnou konvergencí se nemusíme strachovat.

Věta.
Předpokládejme, že posloupnost funkcí { f_k} konverguje stejnoměrně k nějaké spojité funkci f na množině M a že posloupnost funkcí {g_k} konverguje k funkci g na množině N. Předpokládejme dále, že všechny g_k zobrazují N do M. Pak posloupnost { f_k(g_k)} konverguje k f (g) na N.

Teď se podíváme na vlastnosti diskutované výše.

To, že je (iii) tak komplikované, ukazuje, že derivace dokážou být docela zákeřné, dokonce ani stejnoměrná konvergence f_k nestačí k tomu, abychom dostali něco rozumného, je třeba zkoumat derivace. Pak už je to vlastně jen aplikace jisté speciální verze (ii). Protože je ta verze zajímavá sama o sobě, vyslovíme ji.

Tvrzení.
Uvažujme posloupnost funkcí { f_k}, která konverguje stejnoměrně k funkci f na nějakém intervalu M. Předpokládejme, že všechny f_k jsou spojité na M. Zvolme pevně nějaké a z M a pro všechna x z M definujme

Pak F_k konvergují stejnoměrně k F na M.

Víme (viz např. Základní věta kalkulu v části Integrály - Teorie - Úvod), že ty F_k jsou primitivní funkce k f_k a F je primitivní funkce k f. Vidíme tedy, že stejnoměrná konvergence spojitých (tedy integrovatelných) funkcí garantuje konvergenci jejich integrálů a museli jsme uvažovat speciální primitivní funkce, abychom se vyhnuli potížím s konstantami, viz diskuse výše.

Máme také speciální lokální verzi (i), která je někdy užitečná.

Tvrzení.
Uvažujme posloupnost funkcí { f_k} definovanou na nějakém okolí bodu a. Předpokládejme, že pro každé k máme lim_x→a( f_k(x)) = A_k pro nějaké reálné číslo A_k.
Jestliže f_k konvergují stejnoměrně k nějaké funkci f na nějakém okolí a, pak {A_k} je konvergentní posloupnost a lim_x→a( f (x)) = lim(A_k).

Krátce řečeno, (i) a toto Tvrzení říkají, že stejnoměrná konvergence nám umožňuje změnit pořadí limit, jak jsme to diskutovali výše. Podobně (ii) a (iii) říkají, že za příslušných podmínek (stejnoměrná konvergence na správném místě) můžeme měnit pořadí limity a integrování, popřípadě limity a derivování.

Je-li dána posloupnost funkcí { f_k}, můžeme se zeptat na monotonii. Nikterak překvapivě se to dělá bodově.

Definice.
Uvažujme posloupnost funkcí { f_k}, nechť M je nějaká množina, na které jsou všechny f_k definované.
(1) Řekneme, že tato posloupnost je rostoucí na M, jestliže je pro každé x z M posloupnost { f_k(x)} rostoucí.
(2) Řekneme, že tato posloupnost je neklesající na M, jestliže je pro každé x z M posloupnost { f_k(x)} neklesající.
(3) Řekneme, že tato posloupnost je klesající na M, jestliže je pro každé x z M posloupnost { f_k(x)} klesající.
(4) Řekneme, že tato posloupnost je nerostoucí na M, jestliže je pro každé x z M posloupnost { f_k(x)} nerostoucí.
Řekneme, že tato posloupnost je monotonní na M, jestliže splňuje jednu z vlastností výše.
Řekneme, že tato posloupnost je ryze monotonní na M, jestliže je rostoucí na M nebo klesající na M.

Zde to ale vlastně ani není třeba dělat bodově, můžeme pracovat jen s funkcemi jako objekty, protože v sekci Funkce - Teorie - Reálné funkce - Operace s funkcemi jsme definovali srovnání (nerovnost) pro funkce na množině. Takže posloupnost { f_k} je rostoucí na M jestliže f_k+1 > f_k na M pro každé k, podobně můžeme definovat ty ostatní vlastnosti. Je to vlastně totéž, ona nerovnost byla stejně definována skrz body, takhle je to ale schovaně.

Jako příklad si vezměme posloupnost z našeho prvního příkladu (ty mocniny), je klesající na (0,1) a rostoucí na (1,∞). Tato posloupnost už ale není monotonní na (0,∞), protože vzájemný vztah těchto funkcí (směr nerovnosti) je přesně opačný na oněch dvou částech této množiny.

Stejnoměrnou konvergenci studujeme nejraději na uzavřených množinách, protože tam mnoho věcí funguje lépe (všimněte si, že jsme zde také dávali přednost tvrzením s uzavřenými intervaly). Mimo jiné máme na uzavřených intervalech následující zajímavý výsledek.

Řady funkcí
Zpět na Teorie - Řady funkcí