Jedním z cílů kalkulu je schopnost říct co nejvíce o dané funkci. To mimo jiné znamená umět nakreslit její graf tak, aby byly všechny důležité prvky správně. V této sekci identifikujeme ingredience, které nám umožní nakreslit ten správný obrázek. Budeme se soustředit na hlavní myšlenky; detaily o jednotlivých částech se najdou v následujících sekcích.
Správné kreslení průběhu funkce funguje na dvou úrovních. Za prvé je třeba umět řešit částečné úlohy, například jak najít definiční obor, určit asymptoty, zkoumat monotonii atd. Tyto schopnosti se cvičí v jiných částech Math Tutoru. Ale až je zvládnete, je také potřeba umět zkombinovat všechny tyto informace do rozumného celku. Právě to je námětem této sekce.
Poslední poznámka před startem. Níže popsaný proces funguje pro "pěkné" funkce, což v zásadě znamená funkce, jejichž definiční obory lze rozdělit na podintervaly tak, aby byla funkce na každém z nich alespoň dvakrát diferencovatelná (což automatický dává spojitost). Samozřejmě ne každá funkce je taková (viz např. Dirichletovy funkce v části Funkce - Teorie - Elementární funkce), ty se musí zkoumat individuálně.
Vždy začínáme tím, že určíme definiční obor dané funkce f (viz Úvod v části Funkce - Teorie - Reálné funkce nebo Definiční obor v části Funkce - Přehled metod - Základní vlastnosti). To určí náš pracovní prostor a zároveň pomůže s plánováním celkového nákresu, viz níže odstavec o volbě měřítka.
K ukotvení grafu v prostoru používáme body. Obecně čím více, tím lépe, ale nemělo by moc smyslu jen dosazovat náhodně zvolené hodnoty x do f a kreslit body (i když to na druhou stranu neuškodí). Mnohem chytřejší je kreslit body, které jsou něčím významné, kde se něco děje. Dostaneme se k nim za chvíli, zde se podíváme na jeden specifický typ, a to průsečíky se souřadnicovými osami.
Průsečík s osou y najdeme prostě dosazením 0 do f (pokud to
jde).
Průsečík s osou x dostaneme řešením rovnice
Pomůže také vyzkoušet symetrii. Pokud víme, že je funkce sudá či lichá, tak to může ušetřit čas, protože pak stačí nakreslit jen polovinu grafu a doplnit druhou ze symetrie. Nebo se toho dá použít jako bezpečnostní kontrola, udělá se celý graf standardním způsobem a pak se ověří, zda data vyhovují potřebné symetrii.
Někdy zjistíme, že je funkce periodická. To je další ohromná pomoc, protože pak se stačí soustředit na jednu periodu.
Posledním přípravným krokem je prozatímní určení spojitosti na intervalech. Spojitost je pro kreslení grafu podstatná, protože ony nepřerušované části grafu přesně odpovídají intervalům, na kterých je f spojitá. Zatímco pro funkce dané jedním vzorcem to je obvykle jasné (takové funkce bývají spojité na svém definičním oboru), pro grafy funkcí daných rozpisem to bývá zajímavější, viz příslušná sekce. V následujících výpočtech často definiční obor rozdělíme na intervaly a pracujeme s každým z nich zvlášť. Obvykle sice bereme prostě intervaly, ze kterých se definiční obor skládá, ale to funguje jen v případech, kdy tyto intervaly odpovídají spojitosti. Někdy musíme některý z těchto intervalů dále rozdělit podle spojitosti, což se obvykle stává v případě funkce definované po částech, kdy máme rozdílné definice na různých částech určitého intervalu z definičního oboru. Následně proto budeme mluvit o "intervalech z definičního oboru nebo z definice".
Typický graf se skládá z jedné nebo několika nepřerušovaných křivek. Body, které jsme nacházeli výše (průsečíky) a ty z dalších částí nám "ukotví" prostředky těchto křivek, zřídkakdy ale dají informaci o tom, jak tyto kusy vypadají "na konci". Abychom získali tuto informaci, podíváme se na všechny intervaly definičního oboru nebo z definice a najdeme limity v jejich koncových bodech (viz Funkce - Teorie - Limita nebo Funkce - Přehled metod - Limita). Pokud jsou některé koncové body zahrnuty (příslušný interval je tam uzavřený), pak je také důležitá hodnota v dotyčném bodě.
Tuto informaci je možné použít několika způsoby. Za prvé, zhruba nám to říká, kam jdou konce. To se dá dále upřesnit tím, že určíme asymptoty (viz také Asymptoty v části Přehled metod - Průběh funkce). Svislé a vodorovné asymptoty jsou vlastně jen jména pro některé výsledky limit v koncových bodech, pro asymptoty šikmé je ještě třeba trochu pracovat, však také přináší další informaci o tom, jak má graf vypadat.
Informaci o limitách ve vlastních koncových bodech (pokud nějaké jsou) použijeme k určení spojitosti. Na intervaly spojitosti jsme se už dívali, teď máme informaci potřebnou k určení jednostranné spojitosti ve vlastních koncových bodech těchto intervalů a klasifikaci případných nespojitostí. Někdy můžeme zjistit, že některé sousední intervaly spojitosti odhadnuté předtím se vlastně dají spojit do jednoho, což je užitečné vědět, ale v následných výpočtech budeme stejně nejspíše praccovat s takovými intervaly zvlášť, protože důvod, pro který jsme je předtím rozdělili, bude stále hrát roli.
Příklad:
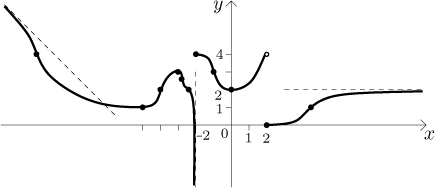
Předpokládejme, že máme funkci f s následujícími údaji: Jako
definiční obor má celou reálnou osu, není symetrická ani periodická.
Průsečíky:
Předpokládáme také, že tato funkce je spojitá na
![]()
Závěry: Máme vodorovnou asymptotu
Funkce je spojitá v −2 zprava a v 2 zprava, má podstatnou nespojitost v −2 a skokovou nespojitost v 2.
To je tedy informace, kterou lze mít v této fázi. Jak ji dáme do obrázku?
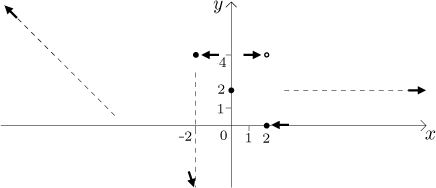
Po dokončení předchozích kroků už víme, kolik nepřerušovaných křivek máme nakreslit a nad kterými intervaly. Díky limitám už také víme, kde tyto křivky končí. Další krok je zjistit, co se zhruba děje mezi konci. První a nejdůležitější věc, kterou musíme zjistit, jsou intervaly monotonie a lokální extrémy, viz další sekce nebo Monotonie a lokální extrémy v části Přehled metod - Průběh funkce).
V typickém případě se intervaly z definičního oboru či definice dále rozdělí na menší intervaly, na kterých už je funkce striktně monotonní. Dozvíme se také, kde jsou "kopečky" a "dolíky" křivek neboli lokální extrémy. Když zaznačíme tyto extremální body, můžeme spojit konce křivek a body grafu dočasnými čárami, dostaneme tak dost dobrou představu o tom, jak graf vypadá.
Příklad:
Předpokládejme, že u předchozího příkladu dostaneme následující tabulku:

a také určíme
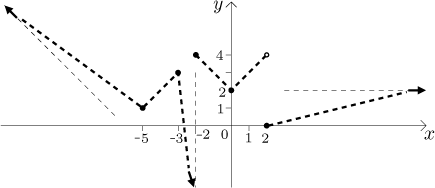
Zbývá už jen graf trochu vyšperkovat, jmenovitě zjistit, jak se kroutí, což je téma další části.
Konvexita a body inflexe (viz příslušná sekce nebo Konvexita v části Přehled metod - Průběh funkce) zpřesňují graf.
Příklad:
Předpokládejme, že v našem příkladě dostaneme následující tabulku

a také určíme
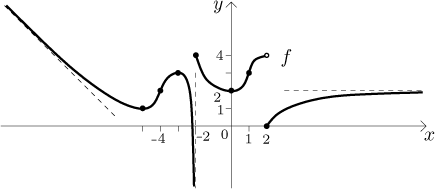
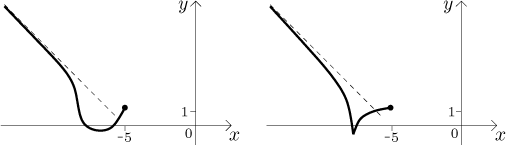
Poznamenejme, že informace o konvexitě je o úroveň důležitosti níže než informace o monotonii. Co tím míníme? Představte si, že máte informaci o konvexitě, tedy znáte intervaly konvexity a inflexní body. Dokážete načrtnout rozumný graf? Odpověď zní, že ne, například v následujícím obrázku mají oba grafy stejné vlastnosti konvexity, ale vypadají dost jinak.
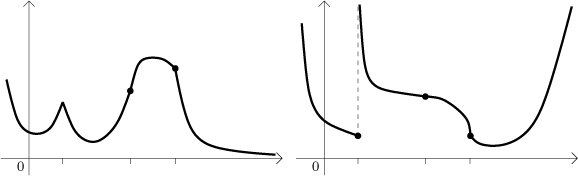
Na druhou stranu, pokud známe monotonii a lokální extrémy, pak už máme docela dobrou představu o funkci, jak už jsme ostatně viděli. Možná nevíme přesně, jak jdou ty tečkované části, ale trendy už tam jsou, konvexita jen udělá obrázek přesnějším. Například v obrázku výše bychom mohli dostat jinou konvexitu a takovýto obrázek.
Všimněte si, že tento obrázek a náš příklad mají stejnou monotonii. Jsou trochu rozdílné, ale ne podstatně, takže změna konvexity už výsledný graf tolik neovlivní.
Když začínáme kreslit graf, tak jedno z prvních rozhodnutí se týká měřítka. Chceme graf, který dává co nejvíce informací, jinými slovy chceme co největší možné měřítko. Pokud je definiční obor "malá" množina, můžeme roztáhnout osu x doširoka, protože nepotřebujeme hodnoty x mimo definiční obor. Druhý důležitý faktor při volbě měřítka jsou body, které budeme zaznačovat (průsečíky, lokální extrémy, body inflexe), protože je nechceme v obrázku příliš namačkané.
Někdy je to snadné, ale můžeme mít situaci, kdy máme několik zajímavých bodů blízko k sobě a pak další zajímavé body docela daleko. Abychom měli v obrázku obě skupiny, potřebovali bychom hrubé měřítko, ale pak se ta těsná skupina bodů objeví příliš blízko na to, aby byla pořádně vidět. Jedním z možných řešení je použít nepravidelné měřítko. V typickém případě bychom použili jemné měřítko v počátku a pak jej postupně dělali hrubším a hrubším, jednou z možností je logaritmické měřítko.
Podobně můžeme mít problém vměstnat do obrázku všechny hodnoty f. To se často napraví tím, že zvolíme rozdílná měřítka pro osy x a y, což zkreslí správný tvar, ale pořád ukazuje důležité informace správně.
Data, která se při kreslení grafu používají, přichází v přirozeném pořadí. Nejprve prozkoumáme samotnou f, jak je popsáno v prvních dvou částech (definiční obor, průsečíky, spojitost, limity, asymptota atd.). Pak se podíváme na derivaci f ′ a dostaneme monotonii a lokální extrémy, pomůže také znát jednostranné derivace v určitých bodech (viz Příklad níže). Nakonec se přejde k druhé derivaci f ′′ a dostaneme informaci o konvexitě.
Ke kreslení grafů jsou v zásadě dva základní přístupy. Jeden přístup je udělat to tak, jak jsme to ukazovali v Příkladě, kdy se dělá obrázek zároveň s výpočty, při každém kroku graf zpřesníme. Druhý přístup je, že nejprve uděláme všechny výpočty a získáme celou informaci. Pak uděláme obrázek ve dvou krocích, abychom je ukázali, znovu nakreslíme tu funkci z Příkladu.
Příklad: Zde použijeme data, která máme výše, k nakreslení grafu jiným způsobem. V prvním kroku dáme dohromady informaci o bodech a limitách/asymptotách, abychom graf ukotvili v prostoru. Dostaneme obrázek podobný tomu, který jsme měli výše po kroku s limitami, ale teď v něm máme také body z dalších dvou kroků (lokální extrémy a body inflexe).

V druhém kroku zkombinujeme do jedné ony dvě tabulky, které jsme měli v krocích o monotonii a konvexitě.

Tato tabulka vyplývá přímo z doporučených metod zkoumání monotonie a konvexity a všimněte si, že už nám dává docela dobrou představu o tom, jak má graf plynout. Teď tento tvar jen "pověsíme" na kotevní body, které už v obrázku jsou, a je to hotovo. Tenhle způsob mám mimochodem raději.

Ať už si vyberete jakýkoliv způsob, je ještě jedna věc, kterou můžete udělat,
abyste měli přesnější graf. Jestliže některé části grafu "končí" ve vlastních
bodech, pak se hodí znát hodnoty jednostranných derivací, abychom to mohli
lépe nakreslit. U toho příkladu výše můžeme předpokládat, že jsme dostali
Poznámka:
Když spojujeme informaci, vyplatí se myslet na to, jak to spolu zapadá. Když
uděláte ve výpočtu chybu, často se to ukáže tím, že dostáváte navzájem sporné
tendence. Například kdyby vám u toho příkladu nahoře daly výpočty, že tato
funkce je konvexní na nějakém intervalu tvaru
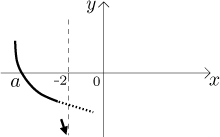
Podobně jakmile víme, že f prochází bodem
Nebo tohle: Když zjistíme, že f má asymptotu
Poznámka: Ukázali jsme, že monotonie je pro tvar mnohem důležitější než konvexita. jinými slovy, dostaneme informaci prvního řádu z první derivace a zpřesníme ji pomocí informace druhého řádu z druhé derivace. Dá se jít dále a zkusit třetí derivaci, abychom dostali informaci třetího řádu, čímž bychom obrázek dále zpřesnili, pak čtvrtý řád atd., čímž by byl obrázek blíž a blíž ke skutečnosti. Bohužel je velice těžké si tyto vyšší řády představit a požívat, protože nejsou spojeny s nějakými jasnými pojmy. Například třetí derivace nám říká, jak rychle se funkce zatáčí v místech, kde je konvexní či konkávní. To se těžce představuje, proto se takovéto informace nepoužívají při hledání průběhu funkce. Tyto informace jsou nicméně podstatné při použití derivací k aproximaci funkcí (viz Taylorův polynom).