Aproximace řad, chyba aproximace

V předchozí sekci jsme viděli, že je obvykle velice obtížné najít přesný součet konvergentní řady. Naskýtá se nápad ji aproximovat sečtením ne všech (tj. nekonečně mnoha) členů, ale jen prvních několika (tisíc, milionů,...). Jak dobrá je taková aproximace? Tato otázka je hlubší, než se zdá.

Předpokládejme, že máme řadu a požádáme počítač, aby sečetl jejích prvních zilión členů. Dostaneme součet 1000. Co si o tom čísle máme myslet? Je řada divergentní (řekněme do nekonečna), ale tak pomalu, že jsme se teprve dostali k 1000, ale později bychom stejně dostali libovolně mnoho? Nebo je konvergentní? Pokud ano, jak blízko její sumě je těch 1000? Na tyto otázky evidentně nelze zodpovědět. Existuje pár triků, ale žádný není příliš spolehlivý. Podívejte se prosím na sekci Numerické výpočty v části Posloupnosti - Teorie - Aplikace pro hlubší náhled; je to o posloupnostech, ale víme, že řady sčítáme zkoumáním posloupností jejich částečných součtů, takže je to velmi relevantní (a dokonce tam klíčový příklad řady používá).

Abychom dostali alespoň nějaké odpovědi, musíme se omezit na konvergentní řady. Začneme tím, že zformulujeme otázku, kterou budeme chtít zodpovědět.

Uvažujme konvergentní řadu  a_k. Pro N > n₀ definujeme . Jestliže součet řady nahradíme tímto částečným součtem, jaká bude chyba? Definujme zbytek

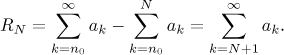
Co o něm můžeme říct? Všimněte si, že když daná řada není konvergentní, tak takový rozdíl dokonce ani nemusí mít smysl. To nás přivádí k našemu prvnímu pozorování. Zdálo by se, že rozhodovat o konvergenci řady, aniž bychom dokázali zjistit, kam vlastně konverguje (což v matematice většinou děláme), je docela na nic, ale teď vidíme, že je to nutný první krok k aproximaci takových součtů pomocí počítačů. Pouze pokud dokážeme, že řada konverguje, má smysl zkoušet nějaké numerické výpočty.

Ale i když takovou konvergenci dokážeme, pořád jsme ještě nepokročili v zjišťování, jak blízko je ten zilióntý součet k součtu nekonečnému. Jedna z možností je nechat si pomoci od integrálního kritéria. Odhad, který tam na konci sekce ukazujeme, se dá přepsat následovně. Jestliže a_k ve skutečnosti pochází z nějaké nerostoucí a kladné funkce f, pak

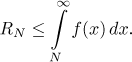
To ještě není přesně to, co bychom potřebovali, protože mnohé řady nesplňují onen poněkud přísný předpoklad tohoto odhadu. Natěstí ale zřídkakdy potřebujeme znát chybu přesně, většinou nám stačí ke štěstí nějaký horní odhad. Za prvé, není opravdu nutné, aby byly všechny členy řady kladné, protože při přechodu k hornímu odhadu můžeme použít absolutní hodnotu. Pak ale výsledná funkce | f | nemusí být nerostoucí. To je ale zase snadné upravit: Protože hledáme horní odhad, můžeme tuto funkci vyhladit, zaplnit její údolíčka, aby se stala monotonní. Dostaneme tak následující.

Fakt.
Uvažujme řadu  a_k, nechť N > n₀. Předpokládejme, že g je nerostoucí funkce taková, že |a_k| ≤ g(k) pro všechna k > N. Pak

To zní dobře, ale není to tak užitečné, jak by se mohlo zdát, protože ne každou funkci g, kterou ukuchtíme, jde rozumně integrovat. Přesto to občas pomůže.

Existuje jeden případ, kdy máme velice snadný a také užitečný odhad pro chybu aproximace - když pracujeme s alternujícími řadami.

Předpoklady této věty mohou dávat lepší smysl, když se porovnají s předpoklady Leibnizova kritéria.

Poznamenejme, že jsme se zde ptali, jak velká je chyba R_N, když sčítáme až po N, ale často je otázka naopak. Je nám dána určitá tolerance E a my potřebujeme vědět, kolik členů řady potřebujeme posčítat, aby tento součet odhadl součet řady v rámci té tolerance E. To znamená, že je třeba vyřešit nerovnost R_N < E pro N a ty odhady výše se pak hodí.

Pro příklady viz Přehled metod - Sčítání řad a Řešené příklady - Sčítání řad, jmenovitě tento příklad a tento příklad.

Absolutní konvergence
Zpět na Teorie - Úvod do řad