Šuplík "substituce"

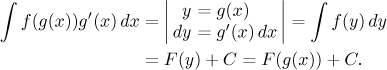
Substituce je metoda, při které v integrálu změníme proměnnou pomocí zvoleného transformačního vzorce, zde budeme přecházet od x k y. Pokud je vzorec ve tvaru y = g(x), jde o substituci přímou, nepřímá substituce vzniká vzorcem h(y) = x a smíšená vzorcem h(y) = g(x). Nejsnadnější je přímá substituce, postup je pak náledující.

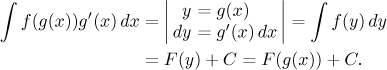
Často však i v případě, že začneme vzorcem y = g(x), ještě musíme pracovat i s jeho upravenými tvary, což pak sklouzává ke smíšené substituci, v praxi se rozdíly z velké části stírají. Uvedeme si proto univerzální algoritmus pro smíšenou substituci, přímá i nepřímá pak budou jen speciální případy.

Algoritmus pro substituci.
Krok 1. Zvolte transformační vzorec h(y) = g(x).
Krok 2. Odvoďte odpovídající transformační vzorec pro diferenciály, h ′(y)dy = g′(x)dx.
Jinými slovy, zderivujte obě strany a připojte odpovídající diferenciály.
Pokud šlo o přímou substituci y = g(x), tak se diferenciály transformují vzorcem dy = g′(x)dx.
Pokud šlo o nepřímou substituci h(y) = x, tak se diferenciály transformují vzorcem h ′(y)dy = dx.
Step 3. Pokud integrál obsahuje výraz g′(x)dx. a mimo něj se proměnná x vyskytuje pouze v rámci výrazu g(x), jděte na další krok.
Jinak použijte vzorce z Kroku 1 a 2 k odvození dalších vzorců, které jsou potřeba pro vyjádření x v intervalu.
Namísto odvozování nových vztahů v Kroku 3 je někdy možné přepsat integrál tak, aby již pasoval ke vzorcům, které již máme z Kroků 1 a 2.
Krok 4. Přepište integrál z jazyka x do jazyka y tak, že nahradíte všechny výskyty x (včetně dx) pouze pomocí vzorců odvozených ze zvoleného transformačního vzorce v předchozích krocích a ničeho jiného. V transformovanékm integrálu nesmí zůstat žádné x. Pokud toto není možné, tak zvolenou substituci nelze provést.
Krok 5. Spočítejte nový integrál, dostanete neurčitý integrál, který používá proměnnou y. Pak udělejte odpovídající zpětnou substituci, tedy odvoďte vzorec pro y ze základní transformačního transformačního vzorce (není třeba, pokud šlo o přímou substituci) a dosaďte za y, čímž se dostanete zpět k jazyku x.

Example: Uvažujte následující výpočet.

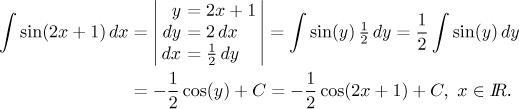
Daný integrál není tabulkový, ale stal by se jím, pokud bychom mohli nahradit člen 2x + 1 písmenem y. To inspiruje naši volbu transformační rovnice, ale ještě nemůžeme provést nahrazení. Potřebujeme totiž nahradit oba výskyty x a k nahrazení dx potřebujeme odvodit příslušný vzorec (Krok 2 výše). Všimněte si, že tento vzorec pochází pouze ze zvolené tranzformace, integrál na to nemá žádný vliv.

Teprve po odvození dy = 2dx je čas jít zpět k našemu integrálu a podívat se, jak nám to spolu zapadá. Odpověď zní, že to moc dobře nesedí, protože v integrálu nemáme 2dx. Je proto čas na Krok 3 neboli přepíšeme naše vzorce do učitečnějšího tvaru, v tomto případě bychom ocenili nějaký vzorec pro d. Naštěstí jej snadno dostaneme.

Máme tedy vhodné vzorce pro nahrazení a provedeme substituci. Jak jsme čekali, dostaneme tak tabulkový integrál, a vyřešíme jej. Nakonec uděláme zpětnou substituci a přidáme nutné části: konstantu C a obor platnosti.

Někdy je možné namísto vytváření nových vzorců vytvořit potřebné výrazy v integrálu chytrým přepisem. Zde je to velmi snadné.

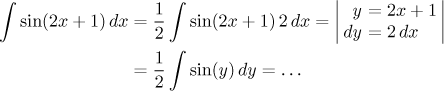
Tento příklad byl extrémně jednoduchý, zkušený integrátor by často rovnou napsal odpověď a výpočty dělal v hlavě, ale ukazuje hlavní prvky substituce. Než se dáme do příkladů, které se zanoří hlouběji do zákrut substituce, podíváme se na jednu důležitou otázku.

Jak volit substituci

Ve většině případů používáme substituci ke zjednodušení složené funkce. V typickém případě se proměnná objevuje v podobě nějakého výrazu g(x), který je dosazen do funkce f. Pokud nahradíme g(x) jen písmenem y, tak se integrál podstatně zjednoduší. Dostáváme se tak k přímé substituci y = g(x). Několik příkladů substitucí, které se tak nabízejí, je zde.

Prvním náznakem, že substituce může být dobrý nápad, je tedy přítomnost složené funkce. To je ale teprve první krok. Víme, že úspěch substituce je určen schopností transformovat všechny výskyty x, největším problémem je diferenciál. Když tedy začneme přemýšlet nad nějakou substitucí y = g(x), tak bychom se měli podívat, jestli je v integrálu také člen g′(x)dx. Pokud tam je, tak substituce nejspíše uspěje.

Shrnuto, pokud daný integrál zahrnuje složenou funkci, tak se podíváme na výraz uvnitř a ověříme, zda se jeho derivace nachází vedle dx. Pokud je odpověď kladná, pak tato substituce bude fungovat. Například bychom určitě použili substituci y = g(x), dy = g′(x)dx u integrálů jako ty následující:

Po substituci z nich budou integrály po řadě z 1/y, yⁿ, sin(y) a e^y.

Nicméně často tomu tak není. Pak se musíme zeptat, jestli se věci nedají alespoň přerovnat tak, aby pasovaly. V mnoha případech to je možné, zejména to vždy platí o lineární substituci y = Ax + B, dx = 1/Ady, viz příklad výše. Pomocí lineární substituce snadno zjednodušíme integrály jako tyto:

Například v následujícím integrálu složená funkce jasně ukazuje na lineární substituci y = 2x − 1 a my už víme, že uspěje, jen je třeba najít vzorec pro x v čitateli.

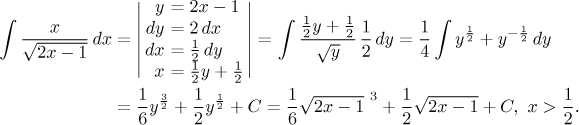
Další integrály, u kterých tvůrčí přístup uspěje, ukazujeme zde. Zkušenost ovšem říká, že pokud je třeba u dx vytvořit něco složitějšího, tak už je to většinou jasné znamení, že dotyčná substituce není dobrý nápad, protože při tom vytváření integrál zase zkomplikujeme. Několik příkladů ukazujeme zde.

Zatím jsme diskutovali přímou susbtituci. Kdy přejdeme ke smíšené? To je ovlivněno funkcí f, některé by se zjednodušily, kdybychom do nich namísto y dali vhodný výraz. Je několik typů integrálů, ukterých víme, že je to dobrý nápad, zejména ty s odmocninami, viz šuplík výše.

Totéž platí pro nepřímou substituci, kterou také používáme pro specifické typy integrálů, viz integrály s odmocninami s kvadráty výše. Nepřímá substituce se snadněji provádí, protože rovnou dává vzorec pro dx, ale mívá potíže se zpětnou substitucí, navíc je třeba si často hlídat, aby použitý vzorec dával prostou funkci. U ní je obzvláště důležité udělat zkoušku.

Příklad: Uvažujme integrál

Je to integrál s odmocninou z kvadrátu a příslušný šuplík radí použít nepřímou substituci x = sin(t), s jejímž provedením tedy nebudou problémy.

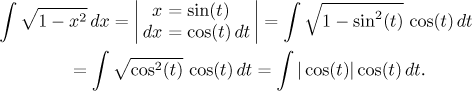
Máme první problém, potřebujeme se zbavit absolutní hodnoty. Víme něco o znaménku kosinu? To visí na otázce, která je pro nepřímou substituci typická, potřebujeme začít řešit intervaly. Původní integrál evidentně existuje na uzavřeném intervalu od −1 do 1 (funkce je tam spojitá), ale co ten nový? Nepřímá substituce vyžaduje, abychom si vybrali nějaký interval, na kterém je sinus prostý a který se zobrazí na interval ⟨−1,1⟩. Kandidáti jsou zjevní a podle toho, který si vybereme, bude určeno i znaménko kosinu.

Zde není důvod vymýšlet něco extra, rozhodneme se pro interval I = . Tam je kosinus nezáporný a absolutní hodnotu můžeme prostě ignorovat. Dostáváme integrál, který patří do šuplíku o goniometrických integrálů, kde se doporučuje použít identity k redukci mocniny, pak už je to snadné.

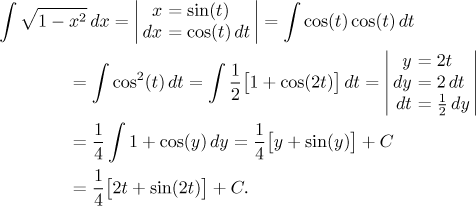
Teď je třeba udělat zpětnou substituci, což je přesně chvíle, kdy se hodí, že na zvoleném intervalu je sinus prostý, proto vyjádříme ze t základního substitučního vzorce pomocí inverzní funkce.

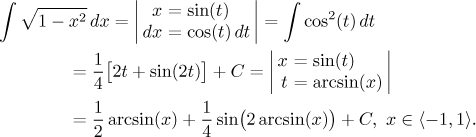
Tento výsledek je sice dobře, ale je zajisté velmi hnusný. Vzhledem k tomu, že se v zadaném integrálu nevyskytují goniometrické funkce, měli bychom se jich ve výsledku snažit zbavit. S tím arcsinem nic neuděláme, ale druhý výraz se dá udělat lépe; jmenovitě ještě předtím, než do sin(2t) dosadíme, si to zkusíme přepsat do výrazu, ve kterém se vyskytuje pouze sin(t) = x.:

Takže (udělejte si zkoušku)

Není to nic pěkného, ale lépe to nejde. Mimochodem, tento integrál je uveden ve všech lepších tabulkách integrálů.

V části Řešené příklady - Integrace většina příkladů používá jako součást řešení substituci, zde vypíchneme zejména tento, tento, tento, tento a tento příklad, v tomto příkladě uvidíte pěknou smíšenou substituci a v tomto pěkný trik se substitucí. Podrobnější pohled na problémy s integračním intervalem v nepřímé substituci pak najdete v šuplíku integrály s odmocninou z kvadrátu.

Další šuplík: per partes
Zpět na Přehled metod - Metody integrace