Příklad: Vyšetřete konvergenci následující řady. (Konverguje? Pokud ano, jak?)

Řešení: Máme se podívat na konvergenci dané řady a také její absolutní konvergenci. Začneme tím prvním. Co se dá říct o členech této řady? Je známo, že sin(k) nabývá kladných a záporných hodnot zcela nepravidelným způsobem, navíc tyto hodnoty nejsou nikdy přesně 1 či −1, funkce sin(x) si prostě vybírá čísla z rozsahu (−1,1), obvykle si vezme tři kladná a pak tři záporná, ale někdy, jen tak aby byla změna a bez nějaké pravidelnosti, si vezme čtyři kladná čísla nebo čtyři záporná za sebou. Rozhodně zde tedy nemáme možnost použít Leibnizovo kritérium a typický kurs kalkulu nenabízí nástroj, kterým by tahle řada šla udolat.

Zde v Math Tutoru jsme zašli trochu dále, některé pokročilejší kursy také zmiňují méně populární ale mocnější testy, mimo jiné jsme tu představili Dirichletovo kritérium. Dá se použít v naší situaci? Čísla b_k = 1/k rozhodně splňují jeho předpoklady, takže zbývá ověřit, že členy a_k = sin(k) tvoří řadu, jejíž částečné součty jsou omezené.

Toje vlastně dobrá otázka. Už jsme připomínali, že obvykle máme tři kladná a pak tři záporná a pak tři kladná čísla a tak pořád dále, občas přijdou čtyři stejná znaménka, zdá se tedy možné, že by se pořád nějak krátily. A to je také pravda, ale dokázat to je něco jiného. Relativně lehké odvození se dá udělat pomocí komplexních čísel a pár známých vzorců, mimo jiné vzorce pro částečné součty geometrické řady.

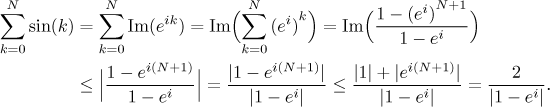
Ukázali jsme, že částečné součty jsou omezeny společnou konstantou, proto daná řada splňuje předpoklady Dirichletova kritéria a jako taková je konvergentní.

Mimochodem, to číslo ve jmenovateli je 2sin(1/2).

Některé lidi ta komplexní čísla mohou odradit a naskýtá se přirozená otázka: Vzhledem k tomu, že náš příklad nemá nic společného s komplexními čísly, je nějaký způsob, jak dokázat omezenost jen pomocí reálných čísel? Vlastně je, ale je přinejmenším tak triková jako ten přístup přes komplexní čísla. Začíná následujícím pozorováním. Jednu konkrétní goniometrickou identitu lze použít k vyjádření sin(k) takto:

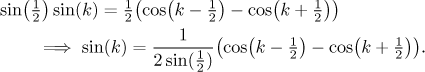
Proč bychom něco takového chtěli? Všimněte si, že jsme sin(k) přeměnili v rozdíl a že takových členů budeme sčítat hodně, což by mělo něco připomenout: teleskopické řady.

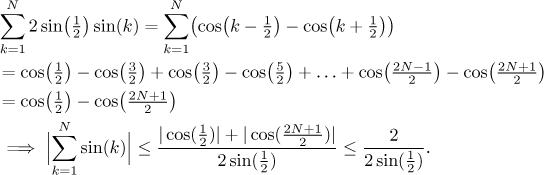
Uf. Nějaký pěkný důkaz neznám. Mimochodem, dostali jsme stejnou horní mez jako u komplexního přístupu.

Teď se podíváme na absolutní konvergenci dané řady. Máme rozhodnout o konvergenci řady

Jaký test nám pomůže? Ten sinus naznačuje, že bychom měli použít srovnání. Dostaneme

Bohužel, ta řada napravo je harmonická řada, jejíž divergence je všeobecně známá, například podle p-testu. Toto srovnání tedy vůbec nepomůže. Připomeňme, že sinus v absolutní hodnotě nabývá hodnot z celého rozmezí (0,1), proto je pro některá k člen |sin(k)|/k v zásadě nula, zatímco pro jiná k je to víceméně 1/k. Jinými slovy, ten odhad použitý před chvílí je tak těsný, jak jen je možné, s horní mezí už níže nemůžeme.

Protože |sin(k)| nemá v nekonečnu limitu, nemá smysl tvrdit, že vypadá pro velká k jako tohle či támhleto, čili není žádná možnost použít limitní srovnání.

Nedostatek konvergence sinové části také vylučuje limitní verze odmocninového kritéria a podílového kritéria. Protože je jasné, že sinus v absolutní hodnotě neumíme integrovat, (a příslušná funkce stejně není nerostoucí), nemůžeme použít ani integrální kritérium a právě nám došly testy. Rozhodně se tedy vyplatí vrátit se k odmocninovému kritériu a podílovému kritériu a popřemýšlet nad jejich obecnějšími verzemi s nerovnostmi.

Za zkušenosti víme, že k ve jmenovateli vůbec nepomůže, protože v obou testech dává 1. To vidíme, když se pokusíme o limitní verze.

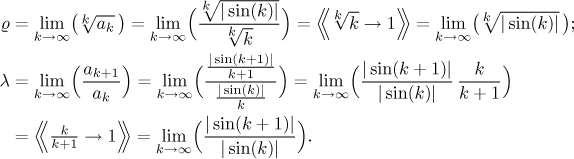
Pokud tedy chceme dokázat nějakou nerovnost, musíme na to použít tu sinovou část. A zde jsme totálně v háji, sinová část není nikdy víc než 1, takže nedokážeme dostat divergenci v odmocninovém kritériu. Na druhou stranu je někdy sin(k) tak blízké jedničce, že [sin(k)]^1/k se také dostane libovolně blízko k 1 a nedokážeme to od 1 oddělit, jak bychom potřebovali pro konvergenci. Nerovnostní verze odmocninového kritéria tedy také nepomůže.

Do podobného průšvihu vletíme také s podílovým kritériem. Podíl sin(k + 1)/sin(k) může být téměř nula, ale také velice velký, rozhodně více než 1. Nejde tedy získat žádnou z nerovností potřebnou pro test.

Právě nám došly testy, které lidé běžně znají, a dokonce ani méně populární testy ze sekce Další kritéria v části Teorie - Testování konvergence nepomohou.

Jsme nuceni přiznat, že testy, které známe, a standardní postupy nejsou dost dobré na rozhodnutí konvergence této řady; to znamená, že zatím nevíme, zda daná řada konverguje absolutně.

Poznamenejme, že kdybychom neměli Dirichletovo kritérium, tak o dané řadě nevíme vůbec nic. Lebnizův test jsme nemohli použít; v takovém případě obvykle přejdeme na absolutní konvergenci, ale zde jsme také narazili. Nástroje, které se tradičně probírají, jsou tedy u tohoto příklady bezmocné. Konvergence se ovšem určit dá, je na to třeba se blíže podívat na danou řadu.

Je to v zásadě harmonická řada, jejíž členy byly modifikovány. Co se s nimi děje? Víme, že pro nekonečně mnoho k jsou čísla |sin(k)| v zásadě 1, takže mnoho členů harmonické řady (o které víme, že diverguje) je v naší řadě zachováno. Na druhou stranu také víme, že sin(k) je prakticky 0 pro nekonečně mnoho k, takže mnoho členů harmonické řady při té modifikaci odpadne. Konvergence či divergence naší řady tedy závisí na tom, jak mnoho členů se (téměř) zachová v porovnání s tím, jak mnoho jich (téměř) vypadne. Jinými slovy, musíme vědět víc o tom, co se děje v tom sinu.

Dobrým začátkem je pozorování, že pro každou malou hodnotu |sin(k)| tam také musí být velká hodnota, takže celkově je tam více "velkých" hodnot než malých. Představte si graf sinu. Jestliže chceme, aby |sin(k)| bylo téměř nula, tak to celé číslo k musí padnout hned vedle nějakého průsečíku grafu sinu a osy x; jinými slovy, k musí v zásadě být nπ pro nějaké celé číslo n. Ale pak musí to další číslo k + 1 padnout poblíž vršku sinové vlny a tudíž z něj musí (po dosazení do sinu) vzniknout relativně velké číslo. Totéž platí pro k − 1, takže opravdu máme víc velkých čísel než "skoro nul" mezi těmi |sin(k)|. To by naznačovalo divergenci (při modifikaci harmonické řady zachováme její velkou část), ale tak daleko ještě nejsme. Zatím jsme ukázali, že "je víc velkých čísel než skoro nul," ale to nám neumožní říct, že řekněme alespoň polovina zkoumané řady jsou velká čísla, protože to zkoumané párování se týká pouze extrémních hodnot, zatímco většina členů v řadě ve skutečnosti padne někam doprostřed - a o těch ještě nic nevíme. Pokud chceme uspět, něco o nich zjistit musíme.

Existují přinejmenším dva způsoby, jak to udělat, dvě možnosti, jak dostat něco hmatatelnějšího. Jedna možnost je všimnout si, že pár k, k + 1 má tu zajímavou vlastnost, že se odpovídající hodnoty vyrovnávají, ať už je jeho pozice vůči sinovým vlnám jakákoliv. Schválně si vemte úsečku o délce 1 (interval ⟨x,x + 1⟩ pro x reálné) a posunujte ji podél osy x v obrázku.

Zdá se, že alespoň jeden konec vždycky dá v sinu velkou hodnotu, někdy oba. Protože nevíme, který konec je ten velký, nejlepší způsob, jak to vyjádřit, je prostě mluvit o součtu těchto hodnot. Tvrdíme, že existuje určité kladné číslo a takové, že součet |sin(x)| a |sin(x + 1)| je vždy přinejmenším a. To se dá dokázat standardními metodami a ta magická dolní mez je ve skutečnosti sin(1), pro detaily viz tato poznámka.

Když máme toto dokázáno, můžeme ukázat, že naše řada diverguje. Nejprve její členy sloučíme do dvojic.

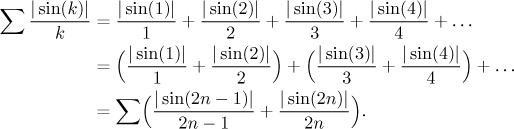
Protože jsou všechny členy kladné, je možné použít asociativní zákon (to není až tak jasné, jak se zdá, viz Základní vlastnosti v části Teorie - Úvod). Konvergence řady nalevo je tedy ekvivalentní konvergenci nové řady napravo. Tam ale můžeme použít srovnání.

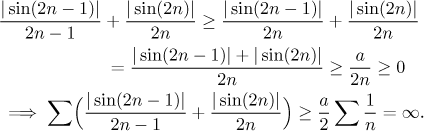
Toto dokazuje, že je řada nalevo divergentní, čili řada s absolutními hodnotami je divergentní, proto daná řada není absolutně konvergentní.
Závěr: Daná řada konverguje neabsolutně.

Alternativa: Když jsme si představovali, co se děje s grafem sinu, tak jsme si mohli všimnout také tohoto: Když si vezmeme tři po sobě jdoucí celá čísla, tak alespoň v jednom z nich je |sin(k)| velké, jmenovitě větší než 1/2. To se dá docela snadno dokázat, viz tato poznámka.

Když máme tohle dokázáno, postupujeme podobně jako předtím. Nejprve spojíme členy řady do trojic.

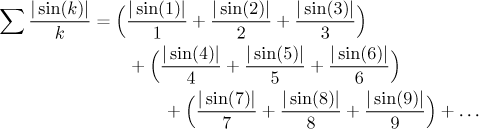
Teď se podíváme na jednu takovou trojici, pro zjednodušení si nahoru dáme nějaké kladné konstanty a díky našemu pozorování víme, že alespoň jedna z nich je větší než 1/2. Můžeme tedy odhadovat

Když toto aplikujeme na rozklad naší řady do trojic, dostaneme

Toto potvrzuje divergenci naší řady.

Takže jsme nakonec vyhráli, ale byla to tvrdá práce. Poznamenejme, že jsou řady, které porazí i ty nejpokročilejší metody a triky, například konvergence či divergence následující řady - ačkoliv je docela pěkná - není stále známa.

(Alespoň nebyla v roce 2004, když jsem se díval naposledy, takže i kdyby to už nebyla pravda, pořád to ukazuje, že i jednoduchá řada jako tato dokáže několik století odolat útokům všech možných testů konvergence a triků.)

Zpět na Řešené příklady - Testování konvergence