Příklad: Vyšetřete konvergenci následující řady. (Konverguje? Pokud ano, jak?)

Řešení: Máme se podívat na konvergenci dané řady a také na její absolutní konvergenci. Začneme tím prvním. Daná řada vypadá jako alternující, ale abychom to potvrdili, musíme ověřit, že ta logaritmická část je vždy kladná. To je snadné, pro kladná celá čísla k je argument 1 + 1/k větší než 1, a tak je logaritmus kladný.

Máme tedy opravdu alternující řadu a můžeme zkusit Leibnizovo kritérium. Čísla

b_k = ln(1 + 1/k)

tvoří klesající posloupnost kladných čísel, která jde k nule. Podle Leibnize daná řada konverguje.

Teď se podíváme na absolutní konvergenci. Víme, že logaritmus je kladný, takže

Začneme podílovým kritériem.

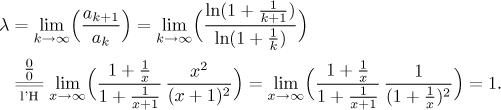
Máme λ = 1, což je neurčitý případ a podílové kritérium nepomůže. Nemá tedy ani smysl zkoušet odmocninové kritérium, protože tam bychom také dostali neurčitý výsledek ϱ = 1. To máme vlastně štěstí, protože odmocninové kritérium by nás uvrtalo do dosti nepěkné neurčité mocniny.

Jaký jiný test by mohl pomoci? Mohli bychom zkusit integrální kritérium, protože funkce ln(1 + 1/x) je kladná a také klesající na intervalu ⟨1,∞). Nejprve zkusíme najít neurčitý integrál, protože to vypadá komplikovaněji a nechceme, aby se nám do toho motaly limity. Asi nejlepší bude se nejdřív zbavit logaritmu pomocí integrace per partes.

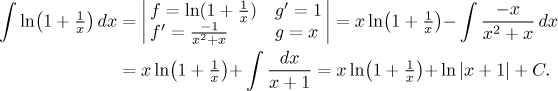
Teď přejdeme na příslušný nevlastní integrál. V limitě bude neurčitý součin, vypořádáme se s ním standardním způsobem.

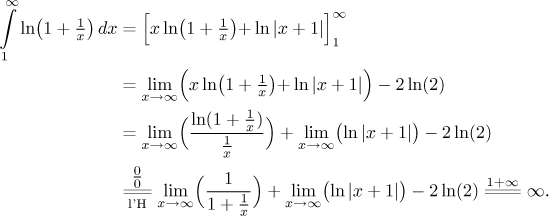
Protože integrál diverguje, také řada, kterou zkoumáme, musí divergovat, tudíž daná řada nekonverguje absolutně.

Zjistili jsme, že řada samotná konverguje, ale není absolutně konvergentní.
Závěr: Daná řada je neabsolutně konvergentní.

Vrátíme se k řadě s absolutními hodnotami a pro úplnost se podíváme na srovnávací kritéria. Jediný evidentní odhad logaritmu je konstantou shora, řekněme ln(1 + 1/k) < 2, ale nekonečná řada dvojek je divergentní , tudíž je takové srovnání na nic. Potřebujeme těsnější, méně velkorysý odhad, ale takové odhady nejsou obecně známy. Možná lepší bude limitní srovnání, takže se zeptáme následující otázku: Když je k velké, jak vypadají naše členy?

Snažší otázka zní: Když je x kladné a velmi malé, jak vypadá ln(1 + x)? Můžeme ten výraz zkusit aproximovat pomocí jeho tečny (viz Derivace - Přehled metod - Aplikace) a dostaneme

ln(1 + x) ∼ x.

Když to aplikujeme na náš případ, dostaneme limitní srovnání, které je třeba ověřit.

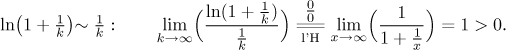
Náš odhad je potvrzen, máme tedy také

Toto potvrzuje, že daná řada není absolutně konvergentní. Mimochodem, ta řada napravo je harmonická řada, jejíž divergence je široce známa, například podle p-testu.

Další příklad
Zpět na Řešené příklady - Testování konvergence