Příklad: Určete, zda následující řada konverguje.

Řešení: Je to evidentně alternující řada, zkusíme Leibnizovo kritérium. Máme

což je posloupnost kladných čísel. Je klesající? Nejjednodušší způsob, jak to poznat, je podívat se na derivaci odpovídající funkce.

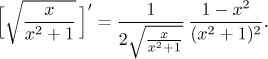
Tato derivace je záporná pro x > 1, a proto ta funkce (a tedy také posloupnost {b_k}) jsou klesající, viz například Monotonie v části Derivace - Přehled metod - Průběh funkce. Tato řada proto splňuje technické předpoklady Leibnizova kritéria a zbývá se podívat na poslední, zda {b_k} jde k 0. To je ale dost jasné, vedoucí mocnina ve jmenovateli je vyšší než mocnina v čitateli, korektní výpočet lze udělat například vykrácením k, viz šuplík o mocninách v nekonečnu v části Posloupnosti - Přehled metod - Limita.

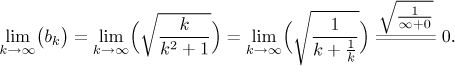
To dokazuje, že podle Leibnizova kritéria daná řada konverguje.

Poznámka: Předvedené řešení je krátké a naprosto postačující, nicméně ze zvědavosti, je nějaká alternativa? Další možnost je zkusit to skrz absolutní konvergenci. Co můžeme říct o této řadě?

Protože se členy této řady skládají z polynomů, tak víme, že jak odmocninové kritérium, tak podílové kritérium nebudou umět rozhodnout. A opravdu,

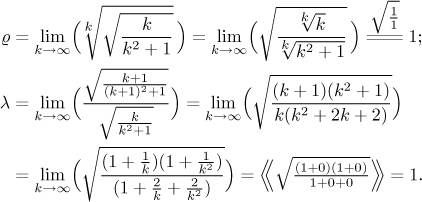
Protože se nám moc nelíbí představa integrovat odmocninu, integrální kritérium je také mimo. Co zbývá? Pro řady s polynomy jsou přece standardním přístupem srovnávaví kritéria.

Jak se řada chová? Když je k velké, tak členy vypadají jako

Všimněte si, že řada napravo je p-řada, která diverguje podle p-testu. To znamená, že už vlastně není třeba dál na srovnávacích kritériích pracovat. Divergentní testovací řada znamená divergentní řadu nalevo. To znamená, že absolutní konvergence, kterou jsme zrovna zkoumali, vyjde negativní: Daná řada nekonverguje absolutně. To je ale přesně situace, kdy nemůžeme říct nic o konvergenci řady původní (máme opačnou implikaci: ještliže řada konverguje absolutně, pak také konverguje). Celý tento přístup k dané řadě přes absolutní konvergenci je tedy slepá ulička a nemá smysl v tom pokračovat.

Pro úplnost ta srovnávací kritéria doděláme. Nejprve uděláme limitní srovnávací kritérium, musíme začít potvrzením správnosti našeho odhadu o chování a_k pro velká k.

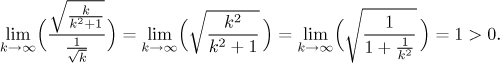
Srovnání je potvrzeno a teď už můžeme dojít k závěru:

Kdybychom zkoušeli přímé srovnání, potřebovali bychom nějakou nerovnost mezi zkoumanými členy a těmi testovacími (či jim podobnými). Jedna se nabízí.

Toto srovnání je ale na nic, protože když je větší řada nekonečná, neříká to ještě nic o menší řadě nalevo. Abychom dokázali, že řada diverguje, potřebujeme dolní odhad. Jeden je možný, ale ten už není tak samozřejmý.

Takže i srovnávací kritérium potvrzuje divergenci (tedy selhání absolutní konvergence) a tím končí ta alternativa, co k ničemu nevedla.

Další příklad
Zpět na Řešené příklady - Testování konvergence