Příklad: Určete, zda následující řada konverguje absolutně.

Řešení: K určení absolutní konvergence bychom měli vzít absolutní hodnotu členů řady, ale ony jsou všechny kladné, a tak na ně nemá absolutní hodnota vliv. Pro tuto řadu je tedy absolutní konvergence ekvivalentní její konvergenci a to umíme (doufejme) určit použitím testů pro řady s nezápornými členy.

Jaký test vypadá dobře? Víme, že když ve členech vystupují jen polynomy a odmocniny, tak nám nepomůže ani odmocninové kritérium, ani podílové kritérium. A moc nám to nevadí, výpočty při zpracování těchto testů by byly dost drsné díky rozdílu ve členech, takže jsme rádi, že to dělat nemusíme.

Jaké máme další testy? Moc se nám nelíbí představa, že bychom členy integrovali, na druhou stranu jsou to jen mocniny a odmocniny, takže by to nemuselo být nemožné. Vzhledem ke zjevným nepříjemnostem s tím spojeným si to raději necháme jako poslední naději, teď se ještě podíváme na zbývající možnost, jmenovitě srovnávací kritéria.

Když se v řadě podíváme po něčem, co lze ignorovat, tak rychle uvidíme, že to není tak jednoduché. Jedno srovnání pomocí nerovnosti je jasné, můžeme ignorovat tu druhou odmocninu, ale tím členy podstatně změníme, což je obvykle jasné znamení, že jsme příliš velkorysí a nebude to k ničemu. A opravdu, dostali bychom

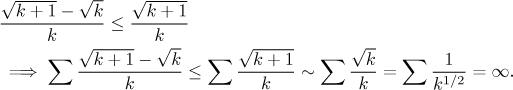
V posledním kroku jsme tvrdili, že část "+1" pro velká k nehraje roli, mohli jsme tedy přejít k řadě, která je divergentní podle p-testu, zde p = 1/2 < 1. Správně bychom ten poslední krok měli udělat pořádně pomocí limitního srovnávacího kritéria, ale není to třeba, protože je to stejně celé k ničemu. Zjistili jsme, že je naše řada omezená shora divergentní řadou, což nám neumožňuje udělat žádný závěr, viz srovnávací kritérium.

Což takhle limitní srovnání? Co se stane, když je k velké? Pokud nahoře ignorujeme to "+1", tak se obě odmocniny vykrátí a dostaneme 0. To je způsobeno tím, že ty dvě odmocniny mají stejné dominantní členy, které se odečítají, a v sekci Intuitivní výpočet v části Posloupnosti - Teorie - Limita jsme odvodili, že v takových případech tento intuitivní přístup selhává. Tudy to tedy nepůjde. Pokud opravdu chceme vědět, co naše členy dělají pro velká k, budeme se nejprve muset zbavit odmocnin algebraicky.

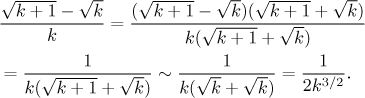
Máme náš odhad a je načase jej potvrdit.

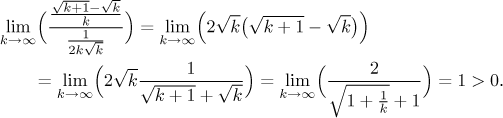
Odhad je dokázaný, teď víme, že

Podle p-testu testovací řada napravo konverguje, proto podle limitního srovnávacího kritéria také daná řada konverguje.

Závěr: Daná řada je absolutně konvergentní.

Pro úplnost si teď vyzkoušíme integrální kritérium. Jsou předpoklady splněny? Funkce, která definuje členy, je kladná, ale její monotonie rozhodně není zjevná. Podíváme se na její derivaci.

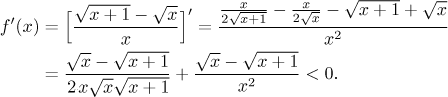
Funkce f je tedy klesající třeba na ⟨1,∞) (viz Monotonie v části Derivace - Přehled metod - Průběh funkce) a můžeme použít integrální kritérium: Namísto dané řady se podíváme na odpovídající nevlastní integrál. Nejprve ale najdeme neurčitý integrál, protože některé části budou jednodušší než jiné. Mohli bychom také rozdělit určitý integrál na několik částí, ale víme, že u nevlastního integrálu si člověk jeho rozdělením na části koleduje o průšvih. Nejprve tedy najdeme primitivní funkci a teprve až ji máme, aplikujeme limity. Jak budeme integrovat? Po malé algebraické úpravě se zbavíme odmocniny substitucí a dorazíme to přes parciální zlomky, viz Integrály - Přehled metod - Metody integrace.

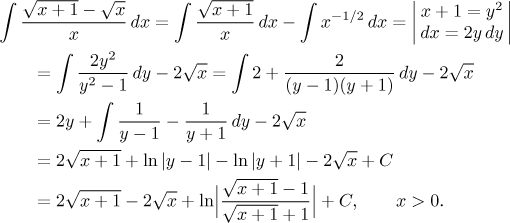
Máme tedy primitivní funkci a teď můžeme přejít k určitému integrálu. Při výpočtu limit budeme mít dva problémy. Logaritmus bude mít uvnitř neurčitý podíl, ale to se snadno vyřeší krácením nejvyšší mocniny ve zlomku, což je odmocnina z x. Ta druhá část, rozdíl odmocnin, také dává neurčitý výraz, a na rozdíl odmocnin máme standardní trik, jmenovitě se jich zbavíme algebraicky. Pro více detailů o těchto fintách viz Limita v části Funkce - Přehled metod.

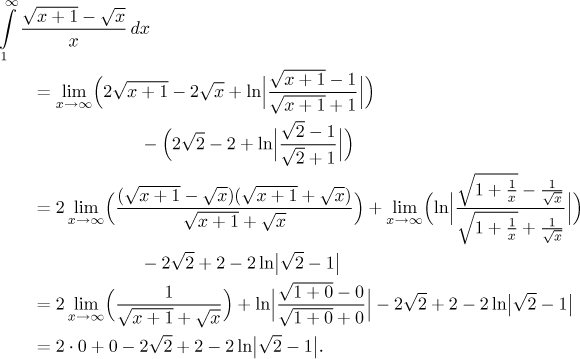
Integrál konverguje, což potvrzuje konvergenci dané řady.

Další příklad
Zpět na Řešené příklady - Testování konvergence