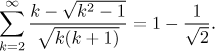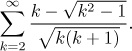
Příklad: Najděte součet řady

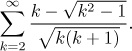
Řešení: Tato řada nevypadá jako něco, co lze přepsat jako geometrickou řadu. Rozhodně také nepochází z nějaké známé nebo jednoduché mocninné řady - už proto, že se v ní nevyskytují členy typu c^k, takže jediná možná mocninná řada, ze které by naše řada mohla vyjít, by musela mít ten komplikovaný zlomek s odmocninami jako koeficient a_k a 1 by se dosazovala do x^k. Upřímně řečeno, nevidím způsob, jak se vypořádat s takovou příšernou mocninnou řadou.

Zbývají tedy dvě možnosti. Buď z toho nějak vyrobíme teleskopickou řadu, nebo ukážeme, že diverguje, čímž se vyhneme nutnosti ji sčítat. Na první pohled ten teleskopický přístup nevypadá moc příjemně, tak se zkusíme podívat na konvergenci. Všechny členy řady jsou kladné (ověřte), takže máme k dispozici spoustu testů. Rozhodně dané členy nechceme integrovat, takže integrální kritérium je mimo hru, a také představa, že hledáme limitu k-té odmocniny z členů zní šíleně, takže je i odmocninové kritérium mimo. Podílové také nevypadá příliš dobře, zbývá tedy srovnání. To není žádný překvapovák, protože máme zlomek s polynomy a odmocninami, přesně ten pravý typ pro srovnání. Jak jednotlivé členy vypadají pro k blízké nekonečnu? Zde máme problém, protože se v čitateli dominantní člen k objevuje dvakrát a odčítá se, což je přesně situace, kdy intuitivní výpočet nefunguje. V takovém případě se musíme zbavit odmocnin v čitateli algebraicky.

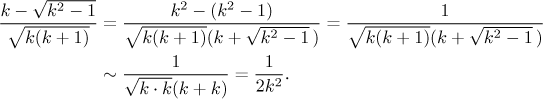
Vidíme, že pro velké k členy řady vypadají v zásadě jako 1/(2k²). To bychom měli potvrdit výpočtem příslušné limity, viz limitní srovnávací kritérium v části Přehled metod - Testování konvergence, ale nemá smysl to dělat. Doufali jsme, že dokážeme, že řada diverguje, ale ona se chová jako řada s členy 1/k², o které víme, že konverguje (viz p-test v části Teorie - Úvod - Důležité příklady nebo příslušný Příklad tamtéž). Zdá se tedy, že naše řada konverguje, a my musíme najít její součet.

Zbývá poslední naděje, potřebujeme přepsat řadu tak, aby měla formu příslušnou teleskopické řadě. Tvar zlomku naznačuje, že bychom jej měli být schopni napsat jako rozdíl, ale potřebujeme zapsat ty dvě vzniklé části tak, aby pocházely ze stejného vzorce, jen s jiným k. Zkusíme to:

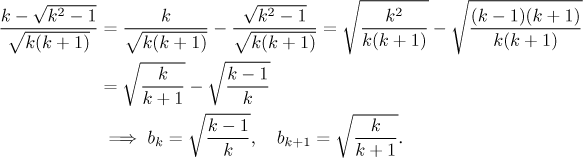
Dostali jsme teleskopickou řadu, takže aplikujeme příslušný postup, jmenovitě se podíváme na její částečné součty.

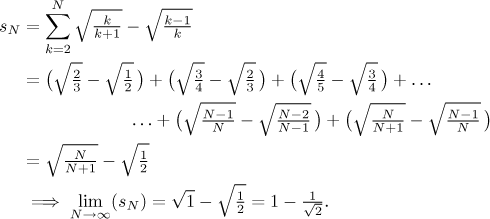
Protože částečné součty konvergují, můžeme prohlásit, že

Další příklad
Zpět na Řešené příklady - Sčítání řad