Příklad: Určete, zda následující řada konverguje.

Řešení: Daná řada je součtem dvou řad. Podíváme se na každou zvlášť a budeme doufat, že ty dva výsledku půjdou dát dohromady.

Nejprve uvažujme řadu

Tuto řadu lze přepsat na geometrickou řadu.

Protože q = 1/5 splňuje |q| < 1, tato řada konverguje.

Teď se podíváme na řadu

Když vidíme faktoriál, hned pomyslíme na podílové kritérium.

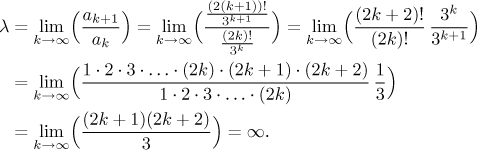
Protože λ >1, tato řada diverguje.

Protože je daná řada součtem konvergentní a divergentní řady, tak je divergentní.

Jsou nějaké alternativy? Co se týče druhé řady, tak je jen jeden další rozumný způsob a je dokonce možná snažší než přístup použítý výše. Víme, že faktoriál přebije exponenciály, proto evidentně členy a_k jdou do nekonečna, takže rozhodně nejdou k nule. Řada pak diverguje podle nutné podmínky.

Jiné testy zde nepomohou. Kvůli faktoriálu nemůžeme integrovat, a tak je integrální kritérium mimo, díky němu je také odmocninové kritérium velmi problematické. A protože tam nejsou části, které by šlo ignorovat, nemá smysl přemýšlet nad srovnávacími kritérii.

Určit konvergenci první řady bylo snadné, ale ze zvědavosti, je nějaká alternativa? Tato řada je zase tak jednoduchá, že není šance ji nějak zjednodušit srovnáním, ale ostatní testy fungují skvěle.

Protože je funkce f (x) = 2/5^x evidentně kladná a klesající na řekněme ⟨0,∞), lze použít integrální kritérium.

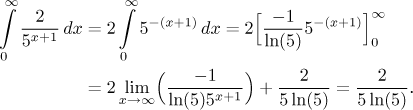
Protože tento nevlastní integrál konverguje, také příslušná řada konverguje.

Také odmocninové kritérium funguje.

Protože ϱ < 1, řada konverguje. Nakonec zkusíme podílové kritérium.

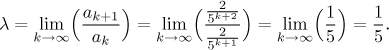
Takže i toto potvrzuje konvergenci (jak se dalo čekat, konstanty v odmocninovém kritériu a podílovém kritériu jsou vždy stejné).

Další příklad
Zpět na Řešené příklady - Testování konvergence