Příklad: Určete, zda následující řada konverguje.

Řešení: Pro kladná celá čísla k je podíl 1/k kladný a nanejvýš 1, takže sinus a obecný člen řady jsou také kladné. Máme tedy řadu s nezápornými členy a můžeme začít přemýšlet nad tím pravým testem.

U téhle řady nevidíme, kudy na ni. Integrace nevypadá snadno, počítat k-tou odmocninu ze sinu také ne, a nejsou tam žádné části, které bychom mohli ignorovat pro srovnání. Kde tedy začneme? Obvykle míváme dobré výsledky s odmocninovým kritériem. Dá se čekat, že sinová část bude působit potíže, jmenovitě vede na neurčitou mocninu. Dá se s tím vyrovnat například takto:

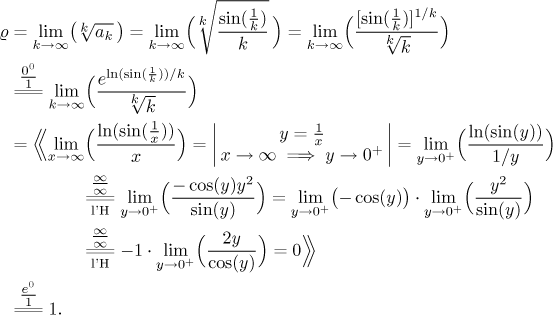
Takže po celé té namáhavé práci máme neurčitý výsledek ϱ = 1. Protože konstanta λ pro podílové kritérium pak také bude 1, nemá to ani smysl zkoušet, ale ze zvědavosti na to jukneme.

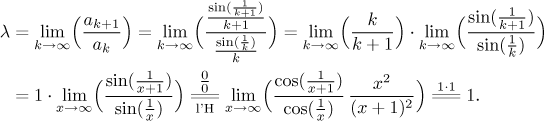
To vlastně vypadalo trochu snadněji. Vzhledem k tomu, že ani tyto dva testy nepomohly, co se dá ještě zkusit? Představa, že daný výraz integrujeme, nezní lákavě, ale pomalu už začínáme být zoufalí a sinus a mocniny nakonec nejsou tak děsné. Můžeme použít integrální kritérium? Ano, protože funkce f (x) = sin(1/x)/x je jak kladná tak klesající na ⟨1,∞). Přejdeme tedy k integrálu a když si jej zkusíte spočítat, dříve či později začnete mít pocit, že metody integrace zde probrané na to nejsou dost dobré. Ve skutečnosti problém není v metodách, ale ve funkci samotné. Jako spojitá funkce má určitě nějakou primitivní funkci, ale je známo, že tuto primitivní funkci nelze zapsat vzorečkem s elementárními funkcemi a operacemi, takže prostě nemůžeme integrovat. Tím končí integrální kritérium, ale mrkněte na Poznámku dole.

Zbývají srovnávací kritéria. Žádnou část výrazu nelze pro velká k ignorovat, ale možná by šel nějaký odhad, sinus má přirozenou horní mez. Pro přirozená čísla k máme, že 1/k leží mezi 0 a 1, takže je tam sinus kladný a my tedy máme

Máme divergentní řadu napravo (je to ta slavná harmonická řada nebo použijte p-test) a daná řada je menší, což je přesně situace, kdy srovnání nepomůže.

Dá se ještě neco dělat? Z našich testů jsme nezkusili limitní srovnání. Moc to na něj nevyp;adá, ale začínáme být zoufalí. Co víme o členech a_k, když se k stane opravdu velkým? Pak je 1/k opravdu malé a pro malá y jsou hodnoty sin(y) v zásadě rovny y. Dá se tedy odhadnout, že

Limitní srovnávací kritérium samozřejmě vyžaduje, že náš odhad ověříme, zvlášť když není zrovna tradiční.

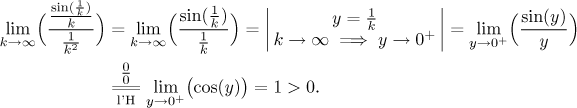
Náš odhad byl správný a můžeme pokračovat se srovnáním.

Protože testovací řada napravo konverguje (viz p-test), platí to i pro řadu nalevo.

Závěr: Daná řada konverguje.

Stejný závěr lze udělat pomocí obyčejného srovnávacího kritéria, ale je na to třeba poněkud zlepšit náš předchozí odhad, ten byl moc velkorysý. Víme, že pro všechna kladná y máme sin(y) < y. Můžeme tedy udělat

a závěr vyplývá z faktu, že větší testovací řada konverguje.

Poznámka. Zde se podíváme blíže na ten integrál z integrálního kritéria. Nejprve si všimněte, že

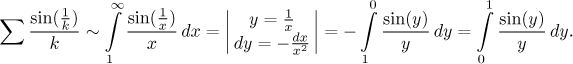
Je dobře známo, že funkce napravo nemá primitivní funkci, kterou by šlo vyjádřit pomocí elementárních funkcí a operací. Zatímco pro "klasickou" integraci tohle znamená konec, můžeme se na to zkusit podívat s využitím mocninných řad. Pomocí standardního rozvoje pro sinus dostaneme

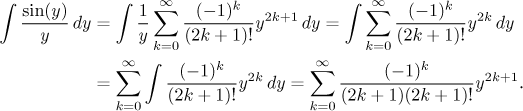
Integrál a sumaci ovšem můžeme prohodit jen na množinách, kde řada konverguje stejnoměrně, viz Řady funkcí v části Teorie - Řady funkcí. Naštěstí pro nás zde máme stejnoměrnou konvergenci na intervalu (0,1⟩, takže onen výsledek je možno použít na libovolném intervalu typu ⟨A,1⟩ pro kladné A, a právě to potřebujeme k výpočtu relevantního nevlastního integrálu.

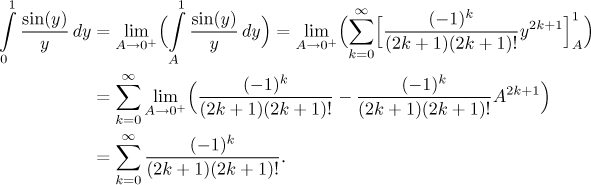
Výsledná řada konverguje, což se snadno ukáže pomocí Leibnizova kritéria. Takže i integrální kritérium potvrzuje, že daná řada konverguje, ale byla s tím spousta starostí, přístup přes srovnání je rozhodně lepší.

Další příklad
Zpět na Řešené příklady - Testování konvergence